CO2 Climate Sensitivity So Low It’s ‘Impossible
To Detect Or Measure In The Real Atmosphere’

“In particular, formula 5 (and 6) as presented here, totally rules out
any possibility that a 33°C greenhouse effect of the type proposed
by the IPCC in their reports can exist in the real atmosphere.”
– Holmes, 2017
In a new peer-reviewed scientific paper published in the journal Earth Sciences last December (2017), a Federation University (Australia) Science and Engineering student named Robert Holmes contends he may have found the key to unlocking our understanding of how planets with thick atmospheres (like Earth) remain “fixed” at 288 Kelvin (K), 740 K (Venus), 165 K (Jupiter)…without considering the need for a planetary greenhouse effect or changes in atmospheric CO2 concentrations.
The Greenhouse Effect ‘Thought Experiment’
Perhaps the most fundamental conceptualization in climate science is the “thought experiment” that envisions what the temperature of the Earth might possibly be if there was no greenhouse effect, greenhouse gases, or atmosphere.
Dr. Gavin Schmidt, NASA
“The size of the greenhouse effect is often estimated as being the difference between the actual global surface temperature and the temperature the planet would be without any atmospheric absorption, but with exactly the same planetary albedo, around 33°C. This is more of a ‘thought experiment’ than an observable state, but it is a useful baseline.”
Simplistically, the globally averaged surface temperature clocks in at 288 K. In the “thought experiment”, an imaginary Earth that has no atmosphere (and thus no greenhouse gases to absorb and re-emit the surface heat) would have a temperature of only 255 K. The difference between the real and imagined Earth with no atmosphere is 33 K, meaning that the Earth would be much colder (and uninhabitable) without the presence of greenhouse gases bridging the hypothetical “heat gap”.
Of that 33 K greenhouse effect, 20.6 K is imagined to derive from water vapor droplets in the atmosphere (1,000 to 40,000 parts per million [ppm] by volume), whereas 7.2 K is thought to stem from the “natural” (or pre-industrial) 200-280 ppm atmospheric CO2 concentration (Kramm et al., 2017).
As a “thought experiment”, the critical heating role for water vapor droplets and CO2 concentrations lacks real-world validation. For example, the Earth’s oceans account for 93% of the planet’s heat energy (Levitus et al., 2012), and yet no real-world physical measurements exist that demonstrate how much heating or cooling is derived from varying CO2 concentrations up or down over a body of water in volume increments of parts per million (0.000001). Consequently, the CO2 greenhouse effect is a hypothetical, model-based conceptualization.
And in recent years, many scientific papers have been published that question the fundamentals of not only the Earth’s hypothetical greenhouse effect, but the role of greenhouse gases for other planets with thick atmospheres (like Venus) as well Hertzberg et al., 2017, Kramm et al., 2017, Nikolov and Zeller, 2017 , Allmendinger, 2017, Lightfoot and Mamer, 2017, Blaauw, 2017, Davis et al., 2018). The Holmes paper highlighted here may just be among the most recent.
‘Extremely Accurate’ Planetary Temperature Calculations With Pressure/Density/Mass Formula
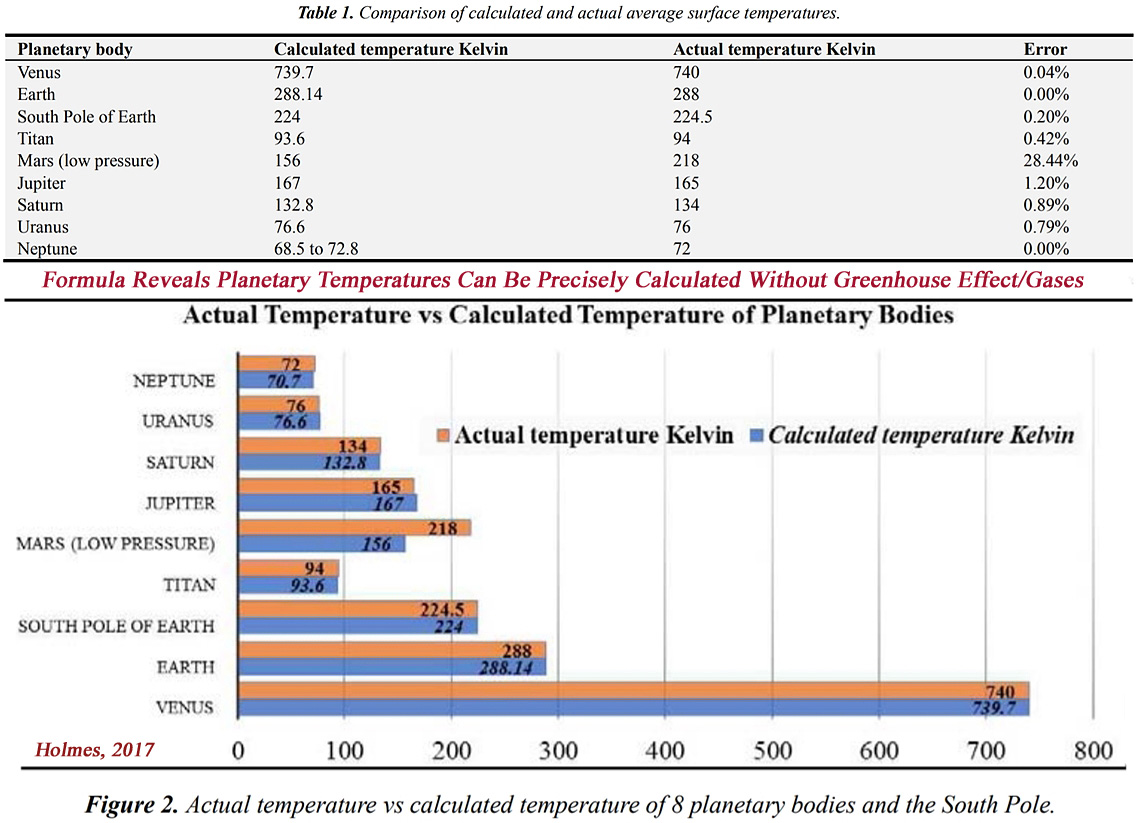
Holmes has argued that the average temperature for 8 planetary bodies with thick (0.1 bar or more) atmospheres can be precisely measured with “extreme” accuracy — an error range of just 1.2% — by using a formula predicated on the knowledge of 3 parameters: “[1] the average near-surface atmospheric pressure, [2] the average near surface atmospheric density and [3] the average mean molar mass of the near-surface atmosphere.”
Holmes used the derived pressure/density/mass numbers for each planetary body. He then calculated the planets’ temperatures with these figures.
Venus’ temperature was calculated to be 739.7 K with the formula. Its measured temperature is 740 K. This indicates that the formula’s accuracy is within an error range of just 0.04% for Venus.
Given Earth’s pressure/density/mass, its calculated temperature is 288.14 K using Holmes’ formula. Earth’s measured temperature is 288 K, an exact fit.
Saturn’s calculated temperature is 132.8 K. Its measured temperature is 134 K — an error range of only 0.89%.
The impressive accuracy of the formula is illustrated below in Table 1. and Figure 2.
Atmospheric Pressure/Density And Surface Temperature
In large part, the density of a planet’s atmosphere is a primary determinant of its temperature. Planets with thick atmospheres are hotter. Planets with thin atmospheres are cooler. The further away from the surface, the less gravity/pressure there is and the cooler it gets. And vice versa.
Sciencing.com
“In general, the weaker the gravitational pull of a planet, the thinner the atmosphere will be. A planet with weak gravity will tend to have less mass and allow more atmosphere to escape into space. Thus the thickness or thinness of the atmosphere depends upon the strength or weakness of gravity. For example, the gravity on Jupiter is 318 times greater than Earth, and thus Jupiter’s atmosphere is much thicker than Earth’s. Gravity gets weaker the further away it is from a planet, so the atmosphere will be thicker near the surface.”
A facile illustration of the effects of atmospheric pressure on the surface temperatures of a planet like Earth can be found in the Grand Canyon, Southwestern U.S. There, the North Rim is about 1,000 feet (305 meters) higher in elevation than the South Rim. Interestingly, the North Rim is also about 9 degrees Fahrenheit colder than the South Rim due to the influence of atmospheric pressure/gravity. The bottom of the canyon reaches temperatures 20-25 degrees warmer than the top. The stark temperature difference is unrelated to the greenhouse gas concentrations for the two locations, nor is it connected to sunlight. It’s the gravitational pressure that creates the heat divergence.
Subia, 2014
“Elevation and season of the year determine average temperatures at the the Grand Canyon. Elevations at top of the South Rim average around 7,000 feet. The North Rim averages about 8,000 feet. The higher the elevation, the cooler the temperature. At any given time, the North Rim will average 8-10 degrees Fahrenheit cooler versus the South Rim. … [T]he very bottom of the canyon can increase 20 to 25 degrees warmer than the top of the respective rims.”
Sensitivity To CO2 Concentration Changes ‘Extremely Low’
Holmes points out that the implications of his precise calculations for planetary temperatures necessarily lead to the conclusion that there is no need to have a greenhouse effect or greenhouse gases to bridge a hypothetical “heat gap.” Instead, he writes that “planetary bodies with thick atmospheres cannot be mainly determined by the ‘greenhouse effect’, but instead most likely by an effect from fluid dynamics, namely, adiabatic autocompression.”
This effectively rules out the possibility that CO2 is a predominant climate driver.
In fact, Holmes’ calculation for CO2 climate sensitivity (doubling the atmospheric CO2 concentration from 0.03% to 0.06%) is -0.03°C.
As he ostensibly understates in his conclusion, “This climate sensitivity is already so low that it would be impossible to detect or measure in the real atmosphere.”
Holmes, 2017
Molar Mass Version of the Ideal Gas Law
Points to a Very Low Climate Sensitivity
Introduction
Presented here is a simple and reliable method of accurately calculating the average near surface atmospheric temperature on planetary bodies which possess a surface atmospheric pressure of over 10kPa [a thick atmosphere, 0.1 bar or more]. This method requires a gas constant and the knowledge of only three gas parameters: [1] the average near-surface atmospheric pressure, [2] the average near surface atmospheric density and [3] the average mean molar mass of the near-surface atmosphere. The formula used is the molar version of the ideal gas law.
It is here demonstrated that the information contained in just these three gas parameters alone is an extremely accurate predictor of atmospheric temperatures on planets with atmospheres >10kPa. This indicates that all information on the effective plus the residual near-surface atmospheric temperature on planetary bodies with thick atmospheres, is automatically ‘baked-in’ to the three mentioned gas parameters.
This formula proves itself here to be not only more accurate than any other method heretofore used, but is far simpler to calculate. It requires no input from parameters previously thought to be essential; solar insolation, albedo, greenhouse gas content, ocean circulation and cloud cover among many others.
Given this, it is shown that no one gas has an anomalous effect on atmospheric temperatures that is significantly more than any other gas.
In short, there can be no 33°C ‘greenhouse effect’ on Earth, or any significant ‘greenhouse effect’ on any other planetary body with an atmosphere of >10kPa.
The Formula: An ‘Extremely Accurate Predictor’ Of Planetary Temperatures






Hi AndyG55 and Steve
Don’t misunderstand, basic physics is fact and is needed to understand the greenhouse effect, so you can’t ignore it. But “not ignore” or “consider it” is logically not equivalent to “be sufficient”. Your statements are not completely wrong but insufficient to explain the observations comprehensive.
Have look on the mean temperature through the atmosphere. Linear increase of the temperature from top to bottom happens only in the so called troposphere close to the surface. That is caused by the convective circulation induced there due to hydrostatic instability of air parcels of different density (via gas law equivalent to different temperature).
But at higher levels the temperature increases again (due to UV absorption of O3, etc.) in the mesosphere and in the thermosphere. Therefore, it is clear that the “APE“, so gas law in gravity field, is insufficient to explain the temperature in the atmosphere completely.
The discussed paper and the claims of some climate deniers on the physical relevance of the “APE” covers only the physical explanation for the linear slope of the temperature through the troposphere. But they fail to address the relevant physical question on what is basically determining the thermal struture of the atmosphere. The reason of the quarrel between scientists and climate deniers is hence not that scientist do not know the basics of their own field resp. refuse to accept simple explanations. The quarrel is caused due to the fact that climate deniers refuse to accept that their explanation is insufficient to explain the temperature of the troposphere completely. With “completely” I mean “down to the fundamental laws of physics”.
As explained above the linear temperature slope results because the air is mixed quasi-adiabatic in the troposphere. But what causes the mixing (= convection)? Convection happen if air is layered instable. This is mostly given in the troposphere and mesosphere but not in the stratosphere and thermosphere. What causes this instability and why does it happen in the troposphere and not in the stratosphere (btw. these spheres are distungiushed due to this fact)? The reason is quite simple but the physics is beyond the playpen climate deniers use to kid the public.
What would happen if no thermal mixing by convection is possible? Well, the air would cool down exclusively by radiating heat radiation into space. It’s self-evident that this process also happen synchronously if convection is possible. But without convection it is the only process how air parcels (and surface) can get rid of heat. If you calculate now the temperature slope through the atmosphere resulting from this radiaton process only you get no linear slope but a bent curve. In the atmospheric layers close to the surface the curve is like this that the air becomes instable and convection is induced. Now you have the physical cause for the convection in the troposphere and the linear slope observed there, it is caused by the physics of the transmission of thermal radiation through the air. If there would be no greenhaouse gases in the air the transmission would be easy: only the solid/liquid surface would emit, therefore no temperature gradient in the atmosphere and therefore no cause for convection and so no linear slope of the temperature.
To make it short: no greenhouse gases = no layered atmosphere and no temperature slope as observed.
roflmao.
What a load of unsupportable anti-scientific rubbish.
Just ignore that basic physics, its what AGW sympathisers have to do.
All increase in lower atmosphere temperature comes from static gravitational compression of that atmosphere as predicted by the ideal gas law itself. The low altitude molecules have decreased mean free path, higher collision rate, thus increased temperature.
While there is sufficient air density for this to happen (above about 0.1bar) the gravity based thermal gradient will exist.
NO REQUIREMENT FOR “RADIATIVE” GASES
There is absolutely ZERO empirical evidence that enhanced atmospheric CO2 causes warming of any sort.
END OF STORY.
Get out of your AGW “fantasy fizzucs” playpen, and meet reality. !!
What is a “climate denier”? How does one go about denying the climate?
So why is it that so many planets’ temperatures cannot be explained by greenhouse gases or solar heat absorption? As scientists say, there is a “major gap” in our understanding” of planetary heating and cooling…and it has not been bridged by greenhouse gases hypotheses.
—
Smith et al., 2007
https://search.proquest.com/openview/cba4766420ef04f09227ccf861784a90/1?pq-origsite=gscholar&cbl=40569
The upper atmospheres of the four Solar System giant planets exhibit high temperatures that cannot be explained by the absorption of sunlight. In the case of Saturn the temperatures predicted by models of solar heating are 200 K, compared to temperatures of 400 K observed independently in the polar regions and at 306 latitude. This unexplained ‘energy crisis’ represents a major gap in our understanding of these planets’ atmospheres. An important candidate for the source of the missing energy is the magnetosphere, which injects energy mostly in the polar regions of the planet. This polar energy input is believed to be sufficient to explain the observed temperatures, provided that it is efficiently redistributed globally by winds, a process that is not well understood. Here we show, using a numerical model, that the net effect of the winds driven by the polar energy inputs is not to heat but to cool the low latitude thermosphere. This surprising result allows us to rule out known polar energy inputs as the solution to the energy crisis at Saturn. There is either an unknown—and large—source of polar energy, or, more probably, some other process heats low latitudes directly.
—
O’Donoghue et al., 2016
http://www.nature.com/nature/journal/v536/n7615/full/nature18940.html?WT.ec_id=NATURE-20160811&spMailingID=52032459&spUserID=Mjg1OTkxNDM2MAS2&spJobID=981769299&spReportId=OTgxNzY5Mjk5S0&foxtrotcallback=true
The temperatures of giant-planet upper atmospheres at mid- to low latitudes are measured to be hundreds of degrees warmer than simulations based on solar heating alone can explain. Modelling studies that focus on additional sources of heating have been unable to resolve this major discrepancy. Here we report that the upper atmosphere above Jupiter’s Great Red Spot—the largest storm in the Solar System—is hundreds of degrees hotter than anywhere else on the planet. This hotspot, by process of elimination, must be heated from below, and this detection is therefore strong evidence for coupling between Jupiter’s lower and upper atmospheres, probably the result of upwardly propagating acoustic or gravity waves.
“This unexplained ‘energy crisis’ represents a major gap in our understanding…”
Yet more proof that the only thing “settled” about this “science” is their ignorance.
Thanks Kenneth!
Hi Kenneth,
>So why is it that so many planets’ temperatures cannot be explained by greenhouse gases or solar heat absorption? As scientists say, there is a “major gap” in our understanding” of planetary heating and cooling…and it has not been bridged by greenhouse gases hypotheses.<
Looking in a textbook about atmospheric physics, meteorology or climate physics it is getting quite clear that atmospheres are more complex then just reducing their thermal structure on the effects of solar radiation and greenhouse gases alone. I gave some examples above already, e.g. ionisation and photo dissociation in the upper earth atmosphere affect the thermal structure there significantly. But nevertheless without greenhouse gases the thermal structure of planetary atmospheres would be completely different then observed. The physics of greenhouse gases (=by definition gases that absorb thermal radiation) is essential to get appropriate physical models explaining the observations quantitatively and allow to evaluate what happen on changed conditions by virtual experiments.
But for e.g. undergraduate lessons simple models only taking radiation transport by greenhouse gases together with the distribution of solar radiation are sufficient to demonstrate the effect of greenhouse gases on the earth troposphere and that they are essential to explain their basic thermal structure. I already explained above that radiation transport by greenhouse gases through the (dense) troposphere causes the convection there. That is a very basic process known in physics since a century or so.
The “major gap” you cited from Smith et al., 2007 and has obviously nothing to do with the physics of greenhouse gases. Indeed there are still challenges to explain the physics of the atmospheres of other planets – especially if the observations are sparse. But it’s self-evident that any quantitative physical model of a planetary atmosphere (earth or Jupiter or…) has implemented an radiation transport through the gas and that the chemical composition and density of this gas affects the radiation transport.
simple models???
Ok stick to what you know.
Easier for you.
Ignore reality.
Hi Kenneth,
so, I guess my explanations referring to the scientific status of knowledge helps a bit to understand why Holmes’ claim is a hoax and to prevents public from junk-science distributed by climate deniers.
It is quite easy for everybody by researching in scentific literature to prove that greenhouse gases are pysically essential to explain the structure of planetary atmospheres.
It can also be verified by any laymen that a first physical approximation of planetary atmospheres (done at Venus, Mars, Titan, …) by so called radiative-convective models give appropriate explanations of observations taken by space probes. Radiative-covective models put the surface albedo, gas composition and their infrared absorption together with the solar irradiation into account, this gives a first guess of the top of troposphere, surface temperature and greenhouse effect (= surface temperature – radiation temperature). So, in this basic question undeniable “scientice is settled” – if one understand science…
Studies of all planets with a viable atmosphere show that the gravity-thermal effect explains all surface temperatures REGARDLESS of atmospheric composition.
There is no empirical evidence that enhanced atmospheric CO2 causes warming of any sort.
The so-called “greenhouse effect” is just a mis-naming of the atmospheric density effect.
You would know that..
…. if you understood science, at all. !!
roflmao….
Ok, what-ever. 😉
Maybe think about what you write next time. !
Uh, no. Your “explanations” did nothing of the kind. Exploring the factors that lead to the temperature gradients for planets like Saturn and Jupiter (no GHGs) is not a “hoax”. Greenhouse theory cannot explain the temperatures of those planets.
And I’ll ask again, What is a “climate denier”? How does one deny the climate?
Then you should be able to easily prove why Jupiter’s temperatures reach 725°C at the top of its atmosphere using greenhouse gases. Please prove this, Markus.
http://jupiter-information-site.weebly.com/jupiters-temperature.html
“At the top of the atmosphere [Jupiter], temperatures can reach as high as 725°C (1,340°F), over 600 miles (1,000 kilometers) above the planet’s surface.”
Please provide the settled-science explanation for why the 4 giant planets’ temperatures are determined by their respective greenhouse gases.
Smith et al., 2007
https://search.proquest.com/openview/cba4766420ef04f09227ccf861784a90/1?pq-origsite=gscholar&cbl=40569
The upper atmospheres of the four Solar System giant planets exhibit high temperatures that cannot be explained by the absorption of sunlight. In the case of Saturn the temperatures predicted by models of solar heating are 200 K, compared to temperatures of 400 K observed independently in the polar regions and at 306 latitude. This unexplained ‘energy crisis’ represents a major gap in our understanding of these planets’ atmospheres.
@Kenneth:
These planets obviously have internal energy sources if they are warmer than expected from the greenhouse effect than the composition of their (detectable) atmospheres.
Yes, some or most of that might come from ongoing compression, since they haven’t yet settled from the formation of our solar system. The rocky planets have definitely settled and their temperatures depend almost exclusively on the Sun and how their atmospheres manage to retain heat by “insulating” the surface. The greenhouse effect.
There is no gravito thermal effect, no “this Holmes paper might have something to it”. It’s BS and a skeptic should be able to identify BS.
@Markus:
don’t get stuck on this blog, they are an almost lost crowd. No matter how often you “explain” stuff to them, they will always hand-wave it away and preach their “skeptic” (or sometimes called “realists”) gospel. Nothing can penetrate their presupposition …