What follows is a wrap up of an article written by skeptic climate and weather site wobleibtdieerderwaermung.de here.
It writes that for thousands of years it has been the solar and ocean cycles that have been influencing the weather worldwide and in Germany.
And looking at data objectively, it is pretty clear that there is little relationship between weather/climate and the rising CO2 concentrations in the atmosphere, as the global warming pause between 1997-2016 shows:
Linear trend of RSS temperatures. No warming in 224 months despite the current powerful El Niño-event. “The least-squares linear-regression trend on the RSS satellite monthly global mean surface temperature anomaly dataset shows no global warming for 18 years 8 months since May 1997, though one-third of all anthropogenic forcings have occurred during the period of the Pause.“ Source: The Pause hangs on by its fingernails.
Naturally climate models continue to grossly overstate the trend for global temperature:
IPCC climate models obviously have assumed an excessively high value for CO2 climate sensitivity. Source: On Natural Climate Variability and Climate Models.
The IPCC climate model projections diverge increasingly from the measured reality, year after year.
In fact new studies have clearly exposed three decisive errors in the programming of climate models:
1. The cooling effect of aerosols has been over-estimated by a factor of 2: Hamburg Max Planck Institute for Meteorology: Aerosols cool less than originally thought.
2. The warming effect of CO2 in in the atmosphere is as a result overestimated by a factor of 2 or three. See: Die kalte Sonne site here (German).
3. The complex effect of fluctuations in solar activity are poorly accounted for in climate models. Solar Forcing of Climate – NIPCC
The consequences: All parameters when used realistically lead to a considerably lower global and regional warming — especially in the future, see following chart:
Source: Peer-reviewed pocket-calculator climate model
It’s time to end the hysteria surrounding CO2 and its grossly exaggerated effects on climate and the ridiculous efforts of protecting the climate on every point on the planet every day for 30 years (whose statistical average is the World Meteorological Organization’s definition of climate). Very little can be accomplished trying, and the price would be enormous and ruinous.
We can argue over whether the pause has ended or not, but one thing is clear: the observations are all well below the model projections.


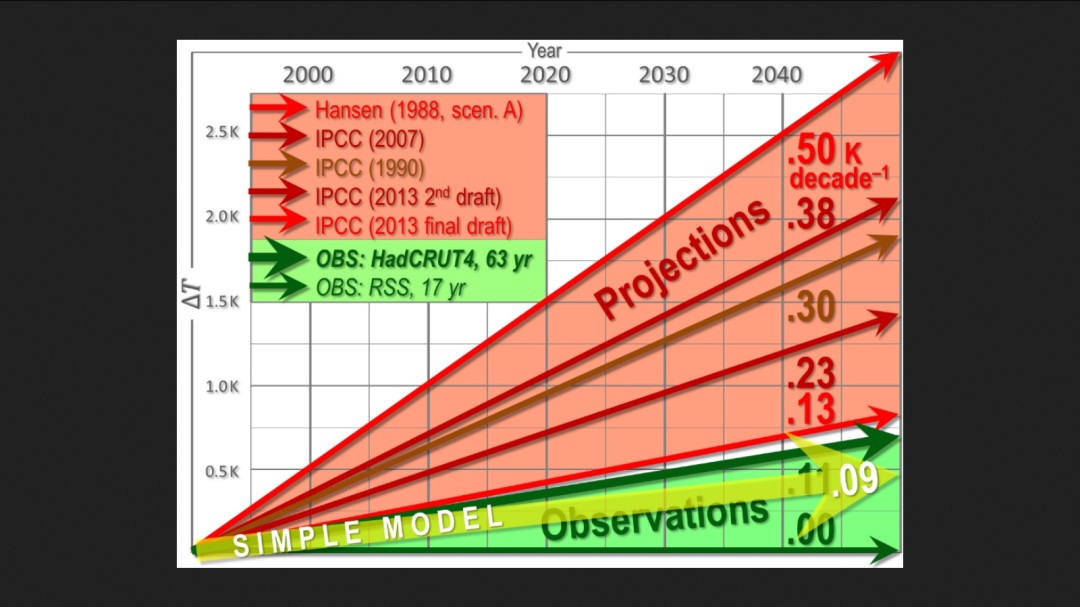





Does anyone know why the extremes of climate model predictions are still presented as possible outcomes?
Check out Monkton’s latest work and paper. The error is apparently in the multiplier factor, or compounding effect, that was actually a model borrowed from the physics of electricity.
A few years ago I was in a shop where the personnel used a book as voluminous as a telephone book to determine their prices depending on two tax tariffs and a list of basic prices from zero to infinity. The same could have been done with a simple formula and a pocket calculator. The bundle of lines from the model runs can indeed be reproduced with a pocket calculator from (1) an estimate of future CO2 level and (2) a CO2 sensitivity parameter (per scenario). The model results are not more true or false than the lines in the book of my shop and only tell in the context of observed temperatures that the sensitivity must be low. If we would use for each year observed temperature and CO2 level, a simple least squares estimate of the sensitivity follows.
sorry, but the pause does no longer hang on its fingernails.
https://wobleibtdieglobaleerwaermung.files.wordpress.com/2016/02/rssglobaltrendpause18jahreund8monatejanuar2016-e1454848951438.jpg
THE PAUSE IS GONE!
http://www.woodfortrees.org/plot/rss/last:236/plot/rss/last:236/trend
Your 1997-present trend shows a trend of about 0.1 C of added “warmth” in 20 years (while CO2 rose by 40 ppm). That’s a trend that’s not even considered statistically significant.
In 1990, the IPCC claimed temperatures would rise at a rate of 0.2 to 0.5 C per decade, with 0.3 C/decade the best estimate. In the last 20 years, temperatures have risen by 0.05 C per decade.
In 2013, the IPCC acknowledged that 111 of 114 climate model simulations did not simulate the 1998-2012 temperature “hiatus” (their word choice). With that kind of a failure rate, why are we even assuming that climate models predicated on CO2 concentrations have any merit?
“In 2013, the IPCC acknowledged that 111 of 114 climate model simulations did not simulate the 1998-2012 temperature “hiatus” (their word choice)”
sorry Kenneth, but you can do better math than this! This claim is obviously bogus and reading the full text shows that your implication is totally wrong.
so you are asking climate models to simulate a specific hand picked period? that is plain out nuts and really fake math at the very best!
KR: “In 2013, the IPCC acknowledged that 111 of 114 climate model simulations did not simulate the 1998-2012 temperature “hiatus” (their word choice)”
———————–
Chapter 9, page 29 of the Final Draft of the AR5 states:
“However, an analysis of the full suite of CMIP5 historical simulations reveals that 111 out of 114 realisations show a GMST trend over 1998–2012 that is higher than the entire HadCRUT4 trend ensemble (Box 9.2 Figure 1a)
“For the period 1998–2012, 111 of the 114 climate-model simulations show a surface-warming trend larger than the observations (Box SYR.1, Figure 1a).”
“During the 15-year period beginning in 1998, the ensemble of HadCRUT4 GMST trends lies below almost all model-simulated trends (Box 9.2 Figure 1a)”
“Almost all CMIP5 historical simulations do not reproduce the observed recent warming hiatus.”
————————
No, I’m just accurately reporting what the IPCC wrote in 2013. Why is it that I know more about what the IPCC report actually said than you do? How embarrassing that you didn’t know that not only did the IPCC acknowledge the “hiatus”, they “hand-picked” the year 1998 as the beginning year for the pause.
By the way, the Hadley Center had the 1998-2012 period showing a cooling trend as of 2012…
https://notrickszone.com/wp-content/uploads/2017/02/HadCRUT-3-vs-4-1998-2012.jpg
So as not to have to deal with explaining this embarrassment (cooling!) for AR5, the HadCRUT dataset was adjusted upwards by +0.1 C in changing the data from HadCRUT3 to HadCRUT4 in 2012 — just in time for the 5th IPCC report. They decided to make the years after about 2003 much warmer than HadCRUT3 had them. That way the trend could tilt upwards rather than downwards. When the data don’t fit the models, just change the data.
Sod,
why did you completely ignore this part from Kenneth?
“Your 1997-present trend shows a trend of about 0.1 C of added “warmth” in 20 years (while CO2 rose by 40 ppm). That’s a trend that’s not even considered statistically significant.
In 1990, the IPCC claimed temperatures would rise at a rate of 0.2 to 0.5 C per decade, with 0.3 C/decade the best estimate. In the last 20 years, temperatures have risen by 0.05 C per decade.”
This was from YOUR chart YOU posted destroying the warmist position,that Kenneth pointed out.
That is why you ignored it,as he destroyed your position. The warming rate is negligible according to your chart YOU made,while the IPCC based on the AGW conjecture,was supposed to warm an average of .30C per decade!
Why continue to embarrass yourself here?
There you go again, proving that you HAVE to use NON-CO2 El Nino transients to find a trend.
You have just PROVEN that if there is any trend, it CAN ONLY be attributed to SOLAR and OCEAN effects.
WELL DONE, sob ! 🙂
“You have just PROVEN that if there is any trend, it CAN ONLY be attributed to SOLAR and OCEAN effects.2
you do not know how to handle data. please start some education.
roflmao.
You have ZERO comprehension of anything to do with maths, or data. I doubt you even passed junior high!
Someone taught you, monkey-like , how to apply a linear trend on data without EVER bothering to actually think about what is really happening.
Are you REALLY just a monkey with a ruler, sob ???
Certainly looks like it. !
You have PROVEN that you just MAKE IT UP as you go along.
PLEASE.. tell us all that El Ninos are caused by CO2, then we can all LAUGH at you…. yet again !!!
You do know that those El Ninos are the ONLY WARMING in the satellite data record… don’t you, little child-mind?
Projections were over a full model run, by the way. Testing them against cherry picked periods of minimum increase is simply a false approach.
Going to be HILARIOUS to watch your childish clown-like attempts at justifying the ever-widening gap over the next several years as temperatures ease down a bit.
please keep going.. it is like watching a petulant child at the start of a tantrum.. totally cringe-worthy;. 🙂
“Going to be HILARIOUS to watch your childish clown-like attempts at justifying the ever-widening gap over the next several years as temperatures ease down a bit.”
yeah, it started already last year, when against all your claims we saw records being broken even in the UAH data.
Somehow you manage to miss the obvious,that major short term warming events have been connected to El-Nino events.
Most of it has already gone away as the atmosphere lost a lot of the “heat” to space and to snow and ice.
CO2 warming signature doesn’t show up,which is why your AGW conjecture is dead!
“Somehow you manage to miss the obvious,that major short term warming events have been connected to El-Nino events. ”
the el nino cycle is part of our climate. you can not simply ignore the data, because you do not like it.
The first graph of this post shows the most absurd abuse of statistics possible you ignore the peak at then end (el nino) and completely destroy the meaning of the data.
“the el nino cycle is part of our climate. you can not simply ignore the data, because you do not like it”
YES.. FINALLY, sob…
Nice to see that you finally realise that the NON-CO2 El Ninos are the only events causing warming since 1979
Well done, sob !!! 🙂
ABSOLUTELY ZERO human warming influence.. all SOLAR and OCEAN CYCLES.
The 1998 El Nino step change is what stops the ZERO back-calculated trend from continuing to the start of the satellite data.
Its the ONLY warming event in the whole of the satellite data set.
And if you really want to see ABUSE of statistics, and manipulation of data..
.. you really do have to look at the NOAA/GISS/BEST fabrications.
You have just ADMITTED that the El Ninos are ALL THAT YOU HAVE…
please, please, sob.. tell everybody that El Ninos are HUMAN driven and not solar, ocean cycle driven.
… that will highlight, to EVERYBODY, your absolutely brain-washed cult belief.
“Nice to see that you finally realise that the NON-CO2 El Ninos are the only events causing warming since 1979”
yeah.
and that is, why you “scpetics” were all predicting that this el nino would break all temperature records.
Oh no, you actually were NOT predicting anything of that kind. Instead you have been shouting “cooling” for a couple of years at the very top of your lungs. Epic fail.
Sod,
Did you just silently admit that CO2 doesn’t drive El-Nino’s?
It is you warmists who scream about record highs,which are based those NATURAL El-Nino events,which have been known to exist for CENTURIES,while making it seem that it was caused by CO2 changes.
CO2 changes doesn’t cause them,for the simple reason that CO2 doesn’t warm ocean waters to warm at all.
You have nothing left,you know it too.
poor little sob still doesn’t understand the word “transient”
Perhaps he will figure it out once he loses his current job abs an inept ignorant troll., and ends up on a park bench rather than his granny’s basement.
Since the models cannot successfully match actual conditions over any period, then what does if we choose a specific range of dates for them to fail over?
Sod,
Modeling runs to year 2100 is scientifically worthless,as they are not testable,therefore not valid.
Short term IPCC claims have already failed spectacularly,yet you continue your pseudoscience charade.
2Modeling runs to year 2100 is scientifically worthless,as they are not testable,therefore not valid.”
No!!! please find out how science works!
Here is the Scientific Method, you never read, Where it shows that a HYPOTHESIS must be tested to determine if the Hypothesis is good or not.
This #3 and #4 from the link:
“Hypothesis – After doing your research, try to predict the answer to the problem. Another term for hypothesis is ‘educated guess’. This is usually stated like ” If I…(do something) then…(this will occur)”
An example would be, “If I grow grass seeds under green light bulbs, then they will grow faster than plants growing under red light bulbs.”
Experiment – The fun part! Design a test or procedure to find out if your hypothesis is correct. In our example, you would set up grass seeds under a green light bulb and seeds under a red light and observe each for a couple of weeks. You would also set up grass seeds under regular white light so that you can compare it with the others. If you are doing this for a science fair, you will probably have to write down exactly what you did for your experiment step by step.”
https://sciencebob.com/science-fair-ideas/the-scientific-method/
It has to be TESTABLE!
“No!!! please find out how science works!”
We can be sure and certain that NOBODY will ever learn how science works from you, sob.
You have made it blatantly obvious that you have ZERO understanding of what science is.
Its almost as if you read all about it in a comic book !
Politicians: Vote for us and we will save you from the ruinous path we are on.
Academia: Fund our projects and we will provide the evidence needed to justify increased taxes and “Save the Planet”.
News Media: We have reports to make – Bad News Sells!!
“Politicians: Vote for us and we will save you from the ruinous path we are on.
Academia: Fund our projects and we will provide the evidence needed to justify increased taxes and “Save the Planet”.
News Media: We have reports to make – Bad News Sells!!”
multi billion dollar fossil fuel industry: we never interfere in anything. Just have a go at it folks!
“multi billion dollar fossil fuel industry”
Which YOU RELY ON, totally and absolutely, for every little part of your meaningless existence. !!
Even though NOAA et al have consistently adjusted upward all recent data and adjusted down all past data they still cannot get their model outputs to approach the adjusted figures
[…] – See more at: https://notrickszone.com/2017/04/08/pause-or-not-climate-models-continue-to-grossly-overstate-global-… […]
Long term thermometer data doesn’t support recent warming
https://co2islife.wordpress.com/2017/03/11/climate-science-on-trial-the-whole-is-greater-than-the-sum-of-its-pieces/
Climate “Science” on Trial; Cherry Picking Locations to Manufacture Warming
https://co2islife.wordpress.com/2017/02/18/a-tale-of-two-cities-cherry-picking-locations-to-manufacture-warming/
Perhaps one of these days, Global Warming Deniers will use real charts based on real observations instead of their fabricated fake charts.
.
Here is the real chart with the real IPCC projection as published in 2007.
http://www.durangobill.com/GwdLiars/Gwd2007IPCC.jpg
The chart above shows what the IPCC really printed in their 2007 report. http://www.ipcc.ch/pdf/assessment-report/ar4/wg1/ar4-wg1-chapter1.pdf (Page 98)
.
And what actually happened?
.
http://www.durangobill.com/GwdLiars/GwdNOAA2016.jpg
(Right down the middle)
According to papers published in Nature, only 2 of 117 climate models accurately projected temperature trends over the 1993-2012 period. That’s a 98% failure rate. Or is a peer-reviewed paper published in Nature too “fake” for you, Bill?
And what’s a “Global Warming Denier”? Are they any different than those who deny the pause/hiatus? Does the site “durangobill.com/G[lobal]w[arming]d[eniers]” have a trustworthy reputation?
——————————–
http://www.blc.arizona.edu/courses/schaffer/182h/climate/overestimated%20warming.pdf
“[W]e find an average simulated rise in global mean surface temperature of 0.30 ± 0.02 °C per decade (using 95% confidence intervals on the model average). The observed rate of warming given above [0.14 ± 0.06 °C per decade] is less than half of this simulated rate, and only a few simulations [2 out of 117] provide warming trends within the range of observational uncertainty (Fig. 1a). The inconsistency between observed and simulated global warming is even more striking for temperature trends computed over the past fifteen years (1998–2012). For this period, the observed trend of 0.05 ± 0.08 °C per decade is more than four times smaller than the average simulated trend of 0.21 ± 0.03 °C per decade (Fig. 1b). It is worth noting that the observed trend over this period — not significantly different from zero — suggests a temporary ‘hiatus’ in global warming
——————————–
http://www.nature.com/nclimate/journal/v4/n3/full/nclimate2111.html
Fyfe et al. showed that global warming over the past 20 years is significantly less than that calculated from 117 simulations of the climate by 37 models participating in Phase 5 of the Coupled Model Intercomparison Project (CMIP5). This might be due to some combination of errors in external forcing, model response and simulated internal variability. … Figure 1 shows observed (red) and simulated (black) trends over the past 20 years (1993–2012) in global mean surface temperature plotted against corresponding trends in eastern tropical Pacific sea surface temperature. As pointed out by Fyfe and colleagues, the observed rate of global warming over this period is less than that simulated in all but two of 117 CMIP5 simulations. Figure 1 shows an even more pronounced discrepancy over the eastern tropical Pacific, with the observed cooling trend being substantially more negative than that in any of the 117 CMIP5 simulations.
Global Warming Deniers are under a delusion that their cherry-picked and fake charts are honest. They are not.
.
Temperature anomalies at all 4 primary temperature databases, the Berkeley Earth Temperature Results, the UAH and RSS satellite interpretations, and Radiosondes (Weather Balloons) are all setting new warmth records.
.
For example, here is the COMPLETE RSS temperature record.
.
Linux LibreOffice Calc Graph: http://www.durangobill.com/TempPictures/RSSanomalies.png
RSS Graph: http://images.remss.com/msu/msu_time_series.html
Data source: ftp://ftp.remss.com/msu/graphics/tlt/time_series/rss_ts_channel_tlt_global_land_and_sea_v03_3.txt
Alternate Data Source: “RSS: Lower troposphere”
http://www.ncdc.noaa.gov/temp-and-precip/msu/overview
What “cherry-picked” and “fake charts” might you be referring to? And why have you decided to make up your own “durangobill” version of the RSS temperature record? Why not use an actual RSS image instead? Like this:
http://images.remss.com/figures/blogs/2014/rss_model_ts_globe_tlt_mears.png
According to the RSS and UAH datasets, temperatures have risen at a rate of 0.12 C per decade since 1979.
According to the IPCC climate models (based on CO2 forcing), temperatures were supposed to have risen at a rate of 0.3 C per decade:
“Based on current model results, we predict: Under the IPCC Business-as-Usual (Scenario A) emissions of greenhouse gases, a rate of increase of global mean temperature during the next century of about 0.3C per decade (with an uncertainty range of 0.2°C – 0.5°C)”
So why do you think it is that the climate models have been so wrong, Bill? Why did only 2 of 117 climate model simulations accurately project temperatures during 1993-2012?
Ken,
it is funny that Bill keeps calling you a Global warming denier,while you have the gall to quote the IPCC and official RSS data to support your position.
You showed a WARMING rate of .12C per decade from 1979,indicating you agree there has been some warming ongoing. You have for a long time known this,thus his attempt to smear you with that name calling, is ignorant and stupid.
“According to the RSS and UAH datasets, temperatures have risen at a rate of 0.12 C per decade since 1979.
According to the IPCC climate models (based on CO2 forcing), temperatures were supposed to have risen at a rate of 0.3 C per decade”
the models model surface temperature, not what the satellites measure.
Come on sob, explain how the surface trend could differ from the lower atmospheric trend
This will be funny.. like all your fabricated nonsense !
“Come on sob, explain how the surface trend could differ from the lower atmospheric trend”
that is a funny question for you to ask.
Please tell me, how the top water layer trend could differ from the surface air trend.
Sod, tries to mislead people with his feeble statement:
“the models model surface temperature, not what the satellites measure.”
The AGW conjecture is based on the ATMOSPHERE,where CO2 molecules are supposed to do its magic in.
Recall the “backradiation” claim.
Recall the Tropical Troposphere warming claim, (hot spot).
Recall that the temperature difference between the Atmosphere and the surface was supposed to be diverging upward over time,by at least THREE TIMES the rate of the surface.
The lower atmosphere is supposed to be getting a LOT warmer,but instead the SATELLITE data show almost zero warming over all.
Here is the telling lower atmosphere chart at Dr. Humlum’s website,where the “hot spot” were supposed to show up:
http://www.climate4you.com/images/EquatorSurface300hPa200hPaDecadalTempChange%20BARCHART.gif
“Diagram showing observed linear decadal temperature change at surface, 300 hPa and 200 hPa, between 20oN and 20oS, since January 1979. Data source: HadAT and HadCRUT4. Click here to compare with modelled altitudinal temperature change pattern for doubling atmospheric CO2. Last month included in analysis: December 2012. Last diagram update: 4 May 2013.”
From this page,
http://www.climate4you.com/
It is warming at less than half the modeled rate,at the 9 kl altitude level,while COOLING slightly at the 12 kl altitude;
Surface is warming a little faster than the lower tropical atmosphere,but those climate models you love so much, says it was supposed to warm around THREE times the rate of the surface.
Lets face it Sod, you have no idea how dumb,ignorant you appear when you keep making foot in the mouth claims.
Both RSS and UAH show only two warming episodes. The first was the 1998 El Nino period, the second was the 2015/16 El Nino transient.
Apart from that there has been NO WARMING AT ALL in either data set.
No warming from 1980-1997
https://s19.postimg.org/iwoqwlg1f/UAH_before_El_nino.png
and no warming from 2001 – 2015
https://s19.postimg.org/b9yx58cxf/UAH_after_El_nino.png
And guess what, bozo-bill, NEITHER of those El Ninos was anything at all to do with anthropogenic CO2, because CO2 cannot and does not cause ocean warming.. that is purely solar effects.
Without using the 1998 El Nino step, and the transient 2015/16…
THERE IS NO WARMING !!
The cheaper the chip, the greater the alarm it can create.
Beware that we are at the end of the pause. Because the models must be true, we will get from now on a giant heating of the earth as compensation in order to attain the climate goals.
“Beware that we are at the end of the pause. Because the models must be true, we will get from now on a giant heating of the earth as compensation in order to attain the climate goals.”
you have zero evidence for such claims.
In the real world, was is happening is the exact opposite:
Roy Spencer was predicting that UAH would not hit a new record, but is own “sceptic2 dataset (with massive changes towards “cooling”) did still confirm what the other datasets say.
“you have zero evidence for such claims.”
There is ZERO evidence that ANY of the model projections approach even closely to REALITY.
There goes that bug-bear of yours, sob
REALITY !!!
Not a realm that you could EVER even pretend to live in.
“There goes that bug-bear of yours, sob
REALITY !!!”
so what did the reality of the UAH data tell us last year?
and what did you predict?
The UAH data indicated that last year (2016) wasn’t statistically warmer than 1998. So what are you trying to suggest here?
http://www.drroyspencer.com/2017/01/global-satellites-2016-not-statistically-warmer-than-1998/
UAH showed everybody that the 2015/2016 El Nino was ONLY a very transient effect, and absolutely NOTHING to do with CO2.
What’s so admirable about you, Sod, is that you always cite the text fragment you want to criticize. Did you acquire this habit in a special course? Anyhow, you knocked me out in one blow. I’m still dizzy. You exposed me with my real name to the whole world. The cited text is the most foolish I’ve ever written. You saw it and had the courage to say it while the others here did nothing.
So a lecturer comes and shows how great the models are at an “open to the public lecture” at our University. Puts up a slide of 14 models with 56 runs over 1880-2010 and says how wonderful the models fit the data. Sigh… says nothing about that this is, maybe 20%, of the models, (the 56 totals runs is just their idea of science as well) hence in reality 80% don’t look good at all.
And people feel ‘re-newed’ in their climate faith.
“So why do you think it is that the climate models have been so wrong, Bill? Why did only 2 of 117 climate model simulations accurately project temperatures during 1993-2012?”
i am starting to worry a little, when i read comments like this one. I actually know of some of you, that you can do better math than this (and on others, i at least hope they can!).
Let us take a model that models 3 big volcanic explosions over a 100 year time frame. It is easy to calculate how often this model will get things right (if we indeed have 3 volcanoes over the next 100 years). You will basically need one million model runs, to just get this simple condition right.
In the real world, the models are a type of pseudo random walk, with the specific purpose of also modelling strange sequences of events. This makes it pretty rare, that a small sample of model runs would perfectly mimic real world data over a stretched period of time.
I am also worried about the strange attitude of dismissing models because they do not perfectly follow reality. That is not how these models work.
In the real world, the most basic (and basically the model of ALL experiments/ scientific approaches) experiment is the “random experiment”, which by nature, is difficult to repeat with the same result.
The arguments brought forward here boil down to this: The professor did roll a die 10 times. I have been rolling all night long, and could not replicate his results. He must be doing fake science!
You very clearly have ZERO comprehension of statistics or mathematics.
Go back to pre-junior high and start again
And FFS .. LISTEN this time !!!
“In the real world, the models are a type of pseudo random walk”
Yes totally random…. affected only by the whims of the designer…
ie pointless, meaningless and a load of GARBAGE !!
multiple replies, zero substance. Is this really all that sceptics have to offer?!?
It is warmists like YOU Sod, who drool over climate models that runs to year 2100,call it credible,then push for huge changes in the way we live based on those models,which are junk since they are NOT testable,therefore not scientific.
CO2 molecules doesn’t warm the Ocean waters at all,neither does it warm the air up since that is being done by energy outflow from the Ocean. It is the SUN that drive the climate,with the Oceans acting like a bellow,occasionally burping out a large heat flux,the energy that originally came from the SUN.
Stop trying to convince many that you are into pseudoscience baloney. I am convinced!
“multiple replies, zero substance.”
You are describing your whole presence here. (and seb’s)
a general, EMPTY yapping.
sob and seb, the flower-pothead men.
I am not expecting “perfect.” For a climate model to have value, however, it should be able to simulate a 15- to 20-year temperature trend. And according to the IPCC and scientists publishing in Nature, the 111 of 114 (or 115 of 117) models failed to simulate temperature trends during 1998-2012 and 1993-2012. That’s a 98% failure rate. Again, not expecting perfect. But a success rate of 2% is worse than guessing. The climate models are junk science.
Various sod’s,
You need to learn the physics of CO2 and quit projecting guilt on to statistical noise. CO2 warms the atmosphere but slightly because it can’t do more. Ninety percent of the electron population resides in the fundamental bend of this molecule. This bend and its constructive and destructive rotational side kicks defines a spectral zone of zero transmission 280ppm. It absorbs so strongly and emits so poorly that surface radiation is extinguished in these bands within a few meters, even at pre industrial levels.
The models fail because they use an emissivity of 1 in the Swartzschild radiative transfer equation, when the highest measured emissivity is.2. Rather than carrying on about inevitable warming because “hey man, it’s a greenhouse gas”; you must explain physically and mathematically how it CAN warm the atmosphere.
A link to the Monckton video seems appropriate here from 2017 Heartland Climate conf. https://www.youtube.com/watch?v=Ebokc6z82cg&t=14s The draws on two findings that explain GCM overestimates, but does not really begin explaining it until 24 minutes in. I believe he also uses an ultra-simplified model of CGMs which correlate with GCM projections to explain it.
Also WattsUp: Part I: How the central estimate of global warming was exaggerated, by Christopher Monckton: https://wattsupwiththat.com/2016/08/27/feet-of-clay-the-official-errors-that-exaggerated-global-warming/
Ceteris Paribus; Less is More, Use Only Data Sets That Don’t Require “Adjustments.”
https://co2islife.wordpress.com/2017/04/09/ceteris-paribus-less-is-more-use-only-data-sets-that-dont-require-adjustments/