Analyses show that global temperatures continue their rapid cooling trend, as Schneefan here writes. What follows are excerpts of his recent comprehensive analysis.
The cooling comes naturally in the wake of the moderate La Nina conditions that have ruled over the past months.
In April surface temperatures 2 meters above the ground plummeted as the following NCEP chart shows:
Source: weatherbell.com/temperature.php
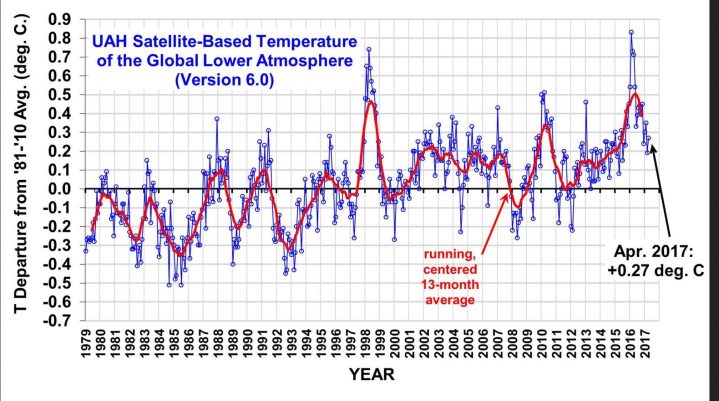
Global satellite temperature anomaly from the mean measured by the University of Alabama in Huntsville (UAH) rebounded a bit after a large March drop.
Source: UAH Global Temperature +0.27 deg. C.
Foremost the atmosphere above the oceans cooled the most during March, 2017. This is clearly depicted by the UAH: an anomaly of +0.29°K to +0.09°K compared to the WMO 1981-2010 mean.
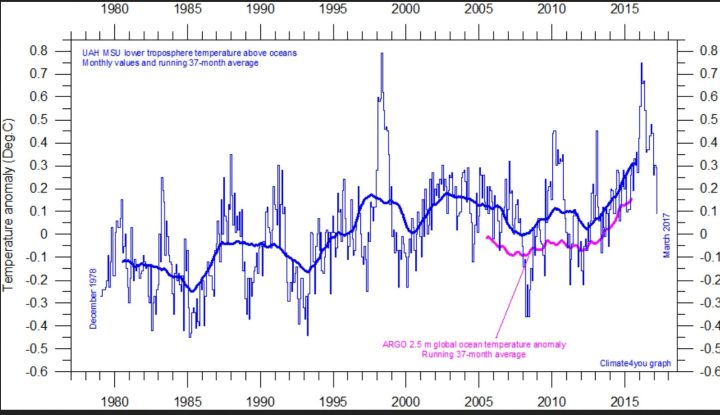
Plot UAH satellite temperatures von UAH in the atmosphere 1500 m altitude (TLT) over the oceans. Note the rose colored curve shows the ARGO ocean buoys’ mean of the sea temperature to a depth of 2.5 m, with 37-month smoothing. Source: www.climate4you.com/, sea surface temperature estimates: UAH.
Global RSS satellite data show a rapid cooling since early 2016:
Moreover despite the powerful warming El Niño event of 2015/16, the unfalsified satellite data in 2016 show that no new significant global heat record was seen when compared to the El Niño year of 1998. We are talking about hundredths of a degree, completely within the boundaries of uncertainty.
No significant warming in 20 years
The powerful linear global cooling continued in April 2017 and will continue for the time being, Schneefan writes.
What does that mean for the global warming? Schneefan adds:
The IPCC global warming claimed by the climate models has been missing for almost 20 years. And that despite the constantly rising atmospheric CO2 concentrations!”
And just days ago, Kenneth Richards here showed that there hasn’t been any warming over the entire southern hemisphere at all. The warming of the past decades is not even global.
What is now becoming glaringly obvious is that the IPCC has wildly overestimated its projected global warming for the future. When the IPCC models from the various IPCC reports are compared to the observations, the result gets vividly illustrated by the following chart showing the satellite observed temperatures from January 2001 to June 2016:
The Global Warming Speedometer for January 2001 to June 2016 shows observed warming on the HadCRUT4 and NCEI surface temperature datasets as below IPCC’s least prediction in 1990 and somewhat on the low side of its 1995 and 2001 predictions, while the satellite datasets show less warming than all IPCC predictions from 1990 to 2001. Later IPCC predictions are too recent to be reliably testable. Source : Is the Reuters “news” agency committing fraud?
Massive Arctic ice thickness growth
The growth in so-called multiyear Arctic sea ice has been considerable over the past nine years. The Chukchi Sea and the East Siberian Sea had little thick multiyear ice back in February 2008. But by February 2017 there was a lot. Massive Growth In Thick Arctic Sea Ice:
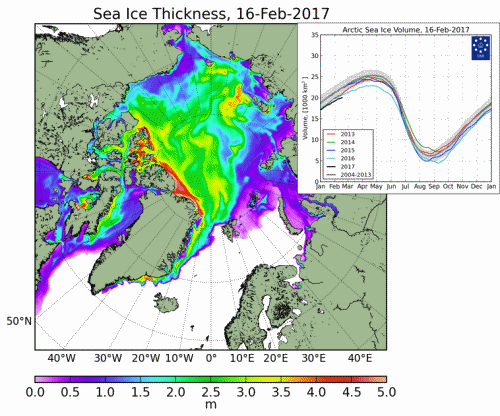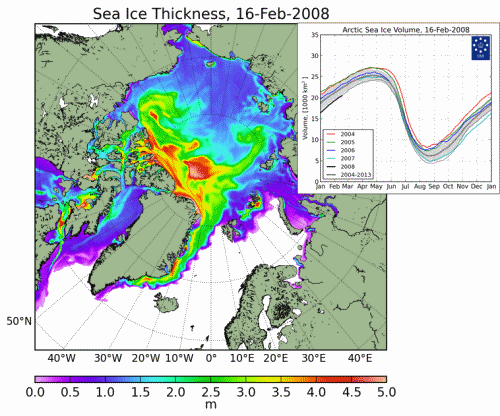
Source: DMI Modelled ice thickness, Real Climate Science.
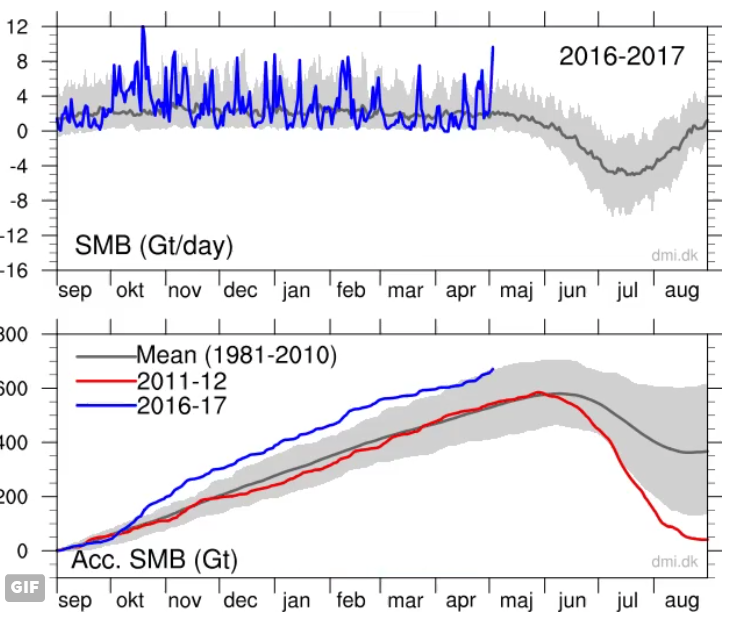
Also Greenland has seen impressive gains in surface snow and ice mass. Kirye at Twitter posted the following chart which shows recent record surface mass gain for 2017:
Source: DMI.
If the Arctic is the climate canary in the coal mine, as many alarmists used to like claiming, then we probably ought to start worrying about cooling.


![The Speedometer for the 15 years 4 months January 2001 to April 2016 shows the [1.1, 4.2] C°/century-equivalent range of global warming rates (red/orange) that IPCC’s 1990, 1995 and 2001 reports predicted should be happening by now, against real-world warming (green) equivalent to <0.5 C°/century over the period, taken as the least-squares linear-regression trend on the mean of the RSS and UAH satellite global lower-troposphere temperature datasets. Quelle: http://joannenova.com.au/2016/05/monckton-ipcc-climate-models-speeding-out-of-control-compared-to-real-world/](https://wobleibtdieglobaleerwaermung.files.wordpress.com/2016/07/klimamodelleabweichungenjan2016bisjunil2016-e1469356263447.jpg?w=720&h=723)





“Massive Arctic ice thickness growth
The growth in so-called multiyear Arctic sea ice has been considerable over the past nine years. The Chukchi Sea and the East Siberian Sea had little thick multiyear ice back in February 2008. But by February 2017 there was a lot. ”
can you please pint out the massive growth in sea ice thickness in the real data?? (2017 in red, 2008 in light blue)
http://psc.apl.uw.edu/wordpress/wp-content/uploads/schweiger/ice_volume/Bpiomas_plot_daily_heff.2sst.png
Russian charts show “old ice” to be:
12% higher than 2016
41% higher than 2008
26% higher than 2009
30% higher than 2012
MASIE shows day 125 sea ice extent above that of:
2006, 2007, 2009, 2010, 2011, 2015 and 2016
real data is, as lways, your enema, sob-sob.
left out 2013, because it was the remnants of a strong weather event..
but in case anyone wants to know… 2017 has some 65% more “old ice” than 2013.
The Arctic sea-ice extent has been running below the 2 sigma range of the satellite era, though it’s been slightly above lately:
http://nsidc.org/data/seaice_index/images/daily_images/N_stddev_timeseries.png
But, notice what happened in 2012, when the previous record minimum was set:
http://nsidc.org/arcticseaicenews/charctic-interactive-sea-ice-graph/
You need to realise that the satellite era started at a rather cold point in time. The end of the “new ice age” scare.
Icelandic records show that Arctic sea ice extent was very high in the late 1970’s up there with the extent of the LIA. !
(can’t access image hosting site at the moment, sorry)
Here’s the image
https://s19.postimg.org/bkgbf2prn/Icelandic_sea_ice_index_2.png
I’m not sure why multiyear ice is even relevant. The DMI graphic above shows Arctic ice volume at The lowest level recorded in the data set. How important is larger patches of multiyear ice if the total ice volume is lower than 2008?
Thanks for your thoughtful comment. multiyear sea ice and thickness are linked.
“sceptics” prefer whatever one is currently higher than at some random moment in time…
a lack of multiyear sea ice shows that the arctic has a serious problem.
a lack of old/thick sea ice makes it vulnerable to massive melting events if weather conditions are right (temperature, wind). it also allows the passage of ships that should not be able to pass.
Why do you put the word “sceptics” in parentheses? Is that because you’d prefer to call those who are skeptical about the narrative that CO2 will cause 10 feet of sea level rise in the next 50 years something else? What are we, then, if we’re not real sceptics?
Did the Arctic have this same “serious problem” during the Early Holocene, when CO2 concentrations were in the 250s ppm?
—
http://www.sciencemag.org/content/333/6043/747.full
Arctic Sea Ice extent during the Holocene Thermal Maximum 8,000 years ago was less than half of the record low 2007 level. [S]ummer sea-ice cover, which reached its Holocene maximum during the LIA, attained its present (~2000) extent at ~4000 years before present. Multiyear sea ice reached a minimum between ~8500 and 6000 years ago, when the limit of year-round sea ice at the coast of Greenland was located ~1000 kilometers to the north of its present position. The subsequent increase in multiyear sea ice culminated during the past 2500 years
—
Why should it be a problem for ships to pass? They were able to do so during Medieval times. Why is that now a bad thing?
Sceptics have an interesting outlook. A year of data starting at the top of an El Nino is a cooling trend but there was no warming on the way up.
It wasn’t called a “trend”. It was called a “cooling”…just as the increase in temperature from the beginning of 2015 to the early months of 2016 was called a “warming”.
You’re making up false statements. No one here has said that the warming during the 2015-’16 Super El Nino had “no warming on the way up”.
If you are going to post here, it would be prudent to accurately represent what others have actually written rather than making up statements and falsely attributing them.
Schneefan got excited over the “strong linear global cooling in 2016” and states “here is no warming (hiatus) from June 1997 to the end of 2015 / beginning 2016. If the global RSS temperatures continue to fall, the “hiatus” will be set and extended again.”
No warming from before the 1998 El Nino to just before the 2016 El Nino, no warming after the El Nino, so how can the Earth be warming? He doesn’t acknowledge the 2015 warming much less run a trendline that includes the 2016 El Nino peak temperature.
El Nino peaks have NOTHING to do with human forced warming.
And it looks like the 2016 El Nino is nothing but a simple transient effect.
If you want to include transient effects and step events to prove “warming” then you are proving SOLAR warming, not human warming
To find a CO2 signature you need to look at periods that don’t include NON-CO2 warming events.
And during those periods.. THERE IS NO WARMING.
Andy there aren’t CO2 and non-CO2 warming events. Every forcing is continually in play affecting global temperatures.
I don’t expect anyone here to say CO2 warmed the Earth in the last decade but admitting there was warming would be nice. The temperature of the lower troposphere rose and at the 2 meter level temperatures rose a lot.
Craig , BELIEVE what you want to believe.
But first show me a paper that proves empirically that CO2 causes warming in a convective atmosphere.
There has been NO WARMING since 2001 except the 2015/2016 El Nino which was an ocean COOLING event.
https://s19.postimg.org/im6e8dgxf/RSS_pre_2015.png
Even that El Nino transient has dropped back down essentially to the pre-El Nino level.
Why should anyone admit there has been warming, when there has demonstrably NOT been. !!
The two m temperature is clouded with MASSIVE uncertainty and unwarranted data manipulation.
It represents barely half the global land mass.
And many of the reporting stations are of highly dubious nature with massive unaccounted for UHI effect, at airports etc etc etc.
The so-called surface data is a JOKE. !!!
https://s19.postimg.org/lcp5couwj/201609_land.gif
UAH TLT data from 1/2001 to 4/2017 shows a trend of +0.09C per decade.
[URL=http://imgbox.com/KuWE3YtB][IMG]https://5-t.imgbox.com/KuWE3YtB.jpg[/IMG][/URL]
http://imgbox.com/KuWE3YtB
Right, and when we start with an El Nino event rather than end with one, the trend is -0.033 C per decade:
http://www.klimatupplysningen.se/wp-content/uploads/2015/05/cooling-1998.jpg
Come off it Craig,
Stop using the El Nino transient to show warming.
Its mathematical nonsense..
Monkey-type application of a tool.
Sort of thing seb would do.
Let’s do an even 20 years and get both El Ninos. The trend from 5/97 to 4/17 is +.055C/decade.
But I’ll admit that strong El Ninos are outliers. What happens if we remove them from the sample? Graphing the last 20 years without the data 6 months either side of the 1998 and 2016 El Ninos gives a trend of +.071C/decade.
http://imgbox.com/L79b8zXg
You have NOT removed them from you calculation.
The way you have drawn it, both El Ninos affect the calculated linear trend… Don’t you realise that ????
To remove the El Ninos you have to split the satellite record into two parts. 1980-1997 and from the culmination of the 1998 El Nino effects in 2001, to the start of the 2015/16 El Nino about half way through 2015
In those two periods, away from El Ninos, THERE IS NO WARMING
https://s19.postimg.org/iwoqwlg1f/UAH_before_El_nino.png
https://s19.postimg.org/b9yx58cxf/UAH_after_El_nino.png
The AGW scammers HAVE to use the 1998 El Nino step change to show a warming trend. Its all they have.
But in doing so they PROVE that the warming was totally natural, and not CO2 related in any way.
Again Andy, right now I don’t care what drove the warming, just that it happened.
Here is a graph of 1980-1997 and 2001 to June 2015.
http://imgbox.com/hfZSVtow
The average LT temperature from 1980 to 1997 was -.11C. Between the start of 2001 to June 2015 the average was 0.13C. How is that possible if no warming took place? Was there some sort of quantum jump from -.11 to .13C?
“Again Andy, right now I don’t care what drove the warming, just that it happened.”
So if you can acknowledge that ENSO events, which are modulated by solar activity, drove the warming, then what exactly are you arguing here? Because that’s what Andy’s saying too.
Or do you really believe that 0.000001 variations (parts per million) in atmospheric CO2 concentrations are drivers of deep ocean water temperature changes…but just don’t want to admit that that’s what you believe here?
Question: if those events are transient, what effect lets the temperatures stay at the higher “step” level years after the event?
It’s true, El Nino events release energy from the oceans into the atmosphere, but it only causes very small dents in the 0-2000m chart, doesn’t it?
https://www.nodc.noaa.gov/OC5/3M_HEAT_CONTENT/heat_content2000m.png
Earth is warming. Atmosphere AND oceans. Denying that isn’t helpful at all (AndyG55).
See, now mention of CO2 at all, but I guess the replies will …
I’m arguing that the Earth warmed in the last 20 years. That seems amazingly hard to get a sceptic to say. The LT averaged 0.24C higher from 2001-2015 than 1980-1997.
ENSO drives the peaks and valleys of the global temperature but by itself the lows will cancel out the highs over a 30 year period. But if you feel that’s why the temperature warmed over the entire satellite record I won’t argue that right now.
In 2014 sceptics were saying that there had been no warming since 1997. Technically it was true, but the scientists knew the next El Nino would change that. Now that it happened there clearly was warming. If sceptics won’t acknowledge that it becomes incredibly hard to carry on a conversation.
“I’m arguing that the Earth warmed in the last 20 years.”
—
http://www.woodfortrees.org/plot/rss/from:1998/to/plot/rss/from:1998/trend
—
According to RSS, it’s “warmed” by slightly less than 0.1 C during the 20 years between 1998 and now. That’s 0.05 C per decade, which is the same rate of decadal warming identified by the IPCC (2013) for 1850-2012 (+0.78 C), and 1998-2012 (0.05 C per decade).
According to IPCC climate models, it was supposed to warm by 0.3 C per decade due to all the alleged CO2 radiative forcing. Why didn’t it? Why did the IPCC have to admit that 111 of 114 climate models didn’t correctly simulate the temperature trends?
—
“In 2014 sceptics were saying that there had been no warming since 1997.”
—
Correct. December, 1997 to December, 2014 showed a cooling of almost -0.1 C:
http://www.woodfortrees.org/plot/rss/from:1998/to:2014/plot/rss/from:1998/to:2014/trend
—
“Technically it was true, but the scientists knew the next El Nino would change that. Now that it happened there clearly was warming.”
—
There clearly was warming due to the onset of the 2015-’16 El Nino.
So you are here acknowledging that the trend changed from -0.1 C cooling to +0.1 C warming because of the natural 2015-’16 El Nino event. So again I ask, if you acknowledge that warming and cooling trends are caused by the presence or absence of a natural ENSO events, what is it you are arguing about with AndyG55? Because that’s what he has been saying too. And if you don’t think the 2015-’16 El Nino changed the trend from cooling to warming, what, exactly, was the cause of the change?
That took awhile but we got there. Warming in the last 20 years.
The reason the climate models didn’t predict the El Nino variations is because they were not built into the model. El Ninos and la Ninas cancel each other out over time.
There was no LT warming from 1997 to 2014 because 1997-98 was an incredibly strong El Nino. Trends for less than 30 years is iffy.
Here is a graph of trends – each point shows the C/decade trend from that date to April 2017. You’ll see a lot of volatility in the 10 – 15 year range but stabilization by the 30 year mark.
http://imgbox.com/Of5wW9wX
Yes, when we add a Super El Nino event to the end, we get a warming “trend” of about 0.1 C in the last 20 years, or 0.05 C per decade. Did you realize that 5/100ths of a degree of warming per decade is not even considered statistically significant? Or does any positive trend line, regardless of statistical significance, count as warming?
Do you have scientific evidence you can cite to substantiate this claim, Craig? I ask because scientists are increasingly finding that temperature variations occur in steps — in sync with ENSO events — and that El Nino events can override La Nina events for “hundreds of years at a time” (leading to more warming, like the Medieval Warm Period) and La Nina events can override El Nino events for “hundreds of years at a time” (leading to cooling, like the Little Ice Age). Please cite scientific evidence to support your claim that El Ninos and La Ninas essentially cancel each other out over time, meaning no net changes in temperature occur due to ENSO factors.
—
Jones and Ricketts, 2017
http://www.earth-syst-dynam.net/8/177/2017/esd-8-177-2017.pdf
“[S]ince the mid-20th century, most observed warming has taken place in four events: in 1979/80 and 1997/98 at the global scale, 1988/89 in the Northern Hemisphere and 1968–70 in the Southern Hemisphere. Temperature is more step-like than trend-like on a regional basis. Satellite temperature is more step-like than surface temperature. … [S]tep-like changes are also present in tide gauge observations, rainfall, ocean heat content and related variables. [A]cross a selection of tests, a simple stepladder model better represents the internal structures of warming than a simple trend, providing strong evidence that the climate system is exhibiting complex system behaviour on decadal timescales.”
“This model indicates that in situ warming of the atmosphere does not occur; instead, a store-and-release mechanism from the ocean to the atmosphere is proposed. It is physically plausible and theoretically sound. The presence of step-like – rather than gradual – warming is important information for characterising and managing future climate risk.” [Climate models predicated on CO2 forcing indicate a gradual, not step-like warming.]
—
https://www.sciencedaily.com/releases/2016/06/160609115117.htm
“El Niño oscillations in Pacific Ocean may have amplified global climate fluctuations for hundreds of years at a time
Scientists have found past El Niño oscillations in the Pacific Ocean may have amplified global climate fluctuations for hundreds of years at a time. The team uncovered century-scale patterns in Pacific rainfall and temperature, and linked them with global climate changes in the past 2000 years. For example, northern hemisphere warming and droughts between the years 950 and 1250 [Medieval Warm Period] corresponded to an El Niño-like state in the Pacific, which switched to a La Niña-like pattern during a cold period between 1350 and 1900” [Little Ice Age].
“El Ninos and la Ninas cancel each other out over time.”
Not recently.
The series of strong solar maximums during the latter half of last century saw to that.
But those maximums seem to have gone…
… and now the energy to charge the El Ninos will take longer to accumulate.
“Here is a graph of 1980-1997 and 2001 to June 2015. http://imgbox.com/hfZSVtow
”
Thanks for the image backing up EVERYTHING I have been saying 🙂
“He doesn’t acknowledge the 2015 warming much less run a trendline that includes the 2016 El Nino peak temperature.”
OMG, a mathematical nonsense.
Of course if you are stupid enough to calculate a trend line using a TRANSIENT spike at the end it will be positive.
The only way you can get a trend is to use that spike.
But that transient spike has now basically dropped back to the pre-spike zero trend.
What is it you are unable to comprehend?
Thanks for the Jones and Ricketts paper Kenneth. I’ll give it a good read.
So can I interpret this (welcome) response to mean that you don’t have anything to substantiate your claim that El Nino warming is cancelled out by La Nina cooling, yielding no net change…and thus temperature trends over the long-term are effectively unrelated to ENSO events? That is what you meant by the “El Ninos and la Ninas cancel each other out over time” comment, right?
No, it means I hadn’t read your paper yet. It says that warming comes in decadal steps rather than a constant increase. (Reminds me of Gould’s punctuated equilibrium) That idea fits the warming of the last 20 years.
“Instead of warming occurring in situ in the atmosphere and/or being released gradually from the ocean, all available heat from additional greenhouse gases not absorbed by the land surface, snow and ice and in lakes is absorbed by the ocean. … The most plausible explanation for step-like behaviour is that steady-state decadal regimes are punctuated by step-like bursts of warming that are subsequently maintained by higher sea surface temperature emplaced by ocean– atmosphere regime changes. This conclusion does not invalidate the considerable literature
that assesses long-term (> 50 years) climate change as
a relatively linear process and the warming response as being
broadly additive with respect to forcing”
If the seas weren’t warming, temperatures after an El Nino would drop back to their previous levels. The paper states as much. “The heat emitted by other El Niño events dissipates and is absorbed back into the ocean within months; thus, an added mechanism is required.”
Craig, did it occur to you that the heat distribution change is an important reason why net warming (or cooling) occurs?
For example, this paper indicates that the ocean surface warming during 1984-2006 could be accounted for by heat distribution changes. If the cooling processes don’t override the warming processes, warming occurs. And vice versa. Understand now?
—
http://journals.ametsoc.org/doi/abs/10.1175/JCLI-D-11-00148.1
“Global satellite observations show the sea surface temperature (SST) increasing since the 1970s in all ocean basins, while the net air–sea heat flux Q decreases. Over the period 1984–2006 the global changes are 0.28°C in SST and −9.1 W m−2 in Q, giving an effective air–sea coupling coefficient of −32 W m−2 °C−1 …[D]iminished ocean cooling due to vertical ocean processes played an important role in sustaining the observed positive trend in global SST from 1984 through 2006, despite the decrease in global surface heat flux. A similar situation is found in the individual basins, though magnitudes differ. A conclusion is that natural variability, rather than long-term climate change, dominates the SST and heat flux changes over this 23-yr period.
—
And what “mechanism” do you believe causes ocean heat content to change over time? For example, notice that ocean heat content plummeted between the Medieval Warm Period and Little Ice Age, and that it has barely risen since then:
https://notrickszone.com/wp-content/uploads/2016/12/Holocene-Cooling-Western-Pacific-Warm-Pool-OHC-2.jpg
So what was the mechanism that caused the cooling, Craig? Is it the same mechanism that caused the tiny +0.09 C of warming between 1955-2010 (Levitus et al., 2012)? Since you don’t think that heat distribution via ENSO has anything to do with net temperature changes in the ocean, what do you think causes net changes in ocean heat? Be specific.
“If the seas weren’t warming, temperatures after an El Nino would drop back to their previous levels”
Umm Craig.. the last two haven’t… 2010, 2015/16.
The 1998 was at the end of a Grand Solar Maximum over the latter part of last century.
And since we know CO2 CANNOT warm ocean water, you are essentially saying exactly we already know.
ITS THE SUN !!!
@sod — The plot you link to is the output of the PIOMAS code. PIOMAS is a _simulation code_; while it is allegedly “data-driven,” its output is still just a _simulation_, not an _observation_. (The technical term that “climate scientists” prefer for a “data-driven” simulation is a “re-analysis,” but the numbers are still just the output of a computer-model, not field measurements or satellite remote-sensing — i.e., PIOMAS “re-analyses” are merely post-hoc _estimates_, not actual empirical observations!)
Moreover, to the best of my knowledge, the source code for PIOMAS has never been released, let alone externally audited, and the papers describing PIOMAS “re-analyses” are more than a little vague about the theory and the “parameterizations” being used within the code. (A “parameterization” is an ad-hoc numerical replacement within a climate simulation for some aspect of climate physics that is either too complex or too poorly understood to be directly calculated — which is another way of saying that it’s a “fudge factor.”)
The PIOMAS “re-analyses” do not appear to be well-calibrated against observation, and appear to contain systematic errors. For example, the correlation coefficient between PIOMAS “re-analyses” and observation is reported in the literature to only be 0.8, and PIOMAS is also reported to systematically underestimate the thickness of thick ice while overestimating the thickness of thin ice — see e.g., Schweiger et al, Journal of Geophysical Research, v.116, p.C00D06 (2011), doi:10.1029/2011JC007084:
http://psc.apl.uw.edu/wordpress/wp-content/uploads/schweiger/pubs/Schweiger-2011-Uncertainty%20in%20model.pdf
Unfortunately, PIOMAS “re-analyses” are nearly always presented _as if_ they were “accurate measurements” of sea ice volume, rather than mere data-driven _simulations_ of sea ice volume.
[…] Data Analyses Show Rapid Global Surface Cooling, Growing Arctic Ice Thickness […]
Northern Atlantic Storm Shows How Natural Causes Affect Arctic Sea Ice
A few years ago the climate alarmists were going hysterical about the sudden loss of Arctic Sea Ice. Alarmist claims of an ice free North Pole dominated the headlines.
https://co2islife.wordpress.com/2017/04/01/northern-atlantic-storm-shows-how-natural-causes-affect-arctic-sea-ice/
If you compare the OSI-SAF web pages for “Ice-type” graphs for 5-4-2017, you will see that the multi-year ice (the portion shaded in white vs. the light gray which is new ice) is about 3 times that of the same graph for 5-4-2007:
5-4-2017:
http://osisaf.met.no/p/osisaf_hlprod_qlook.php?year=2017&month=05&day=04&prod=Ice-Type&area=NH&size=25%25
5-4-2007:
http://osisaf.met.no/p/osisaf_hlprod_qlook.php?year=2007&month=05&day=04&prod=Ice-Type&area=NH&size=25%25
The only years that come close to 2017 since 2007 is 2010 and 2014.
By the way, does anyone know why DMI has not updated their arctic temperature graph since Tuesday? (“Temp Arctic DMI” link under “Climate Indicators” to the right)
I’ve been asking them all week.
I smell a rat it looked like it was going to head due east on the chart and then poof no data.
Whatever the problem, the data is now up.
http://ocean.dmi.dk/arctic/meant80n.uk.php
If you are interested in the real data instead of the fake data in the article, here’s the real data.
Polar Science Center
University of Washington
Arctic Sea Ice Volume Anomaly
http://psc.apl.uw.edu/research/projects/arctic-sea-ice-volume-anomaly/
http://psc.apl.uw.edu/wordpress/wp-content/uploads/schweiger/ice_volume/BPIOMASIceVolumeAnomalyCurrentV2.1.png
Bill,
“If you are interested in the real data instead of the fake data in the article, here’s the real data.”
By what method are YOU able to differentiate so called ‘fake data’ from so called ‘real data’? Surely you are just espousing bias.
“If the Arctic is the climate canary in the coal mine, as many alarmists used to like claiming, then we probably ought to start worrying about cooling.”
the arctic is not looking good for “sceptics”. You are trying to trick people into thinking so, by choosing the few data points and datasets that support this false perception. This will not work in the long run.
Arctic is looking wonderful
It has recovered somewhat from the extremes of the late 1970’s, back down slightly towards a more normal level for the Holocene
Even after the natural drop ,
Russian charts show “old ice” to be:
12% higher than 2016
41% higher than 2008
26% higher than 2009
30% higher than 2012
and around 65% higher than 2013
MASIE shows day 125 sea ice extent above that of:
2006, 2007, 2009, 2010, 2011, 2015 and 2016
And this is after the “less cold” blob that was over the Franz Joseph region for much of freeze up period.
(Which incidentally sent an anomalous cold blob over northern Russia, where people actually live, as if the likes of slimebags like sob could care about human struggles)
REAL DATA shows that sob-sob’s chicken-little Arctic cry-baby routine is all coming apart on him.
No wonder he is so close to tears all the time.
poor sob-sob.
EVERY bit of available evidence points to the Arctic behaving totally normal.
Still very much on the high side compared to the rest of the Holocene, higher than it has been for 95% of the last 10,000 years.
Only person choosing data points is you and your Arctic cry-babies, choosing just the period since the EXTREMES of the late 1970’s.
And you know that is the FACTS, sob-sob..
According to HadCRUT4 data (that the IPCC uses) the Arctic has had no net warming in 80 years. Is that good for skeptics or is it good for the climate worriers?
https://notrickszone.com/wp-content/uploads/2017/04/Arctic-Temperatures-1920-2017-HadCRUT4.jpg
If its looking good for AGW scammers, I expect we will see sob-sob moving out of his inner-city ghetto basement (heated by fossil-fuels) and moving to Iceland or Siberia, where the heat isn’t so oppressive.
Waiting, waiting..
or will he remain a total hypocrite.;-)
Kenneth, you keep linking the same garbage graph.
That graph shows massive fluctuations in the past, about twice the size that fluctuations are today.
Either the world was completely different back then or that data is simply garbage. Your choice.
https://notrickszone.com/wp-content/uploads/2017/04/Arctic-Temperatures-1920-2017-HadCRUT4.jpg
I link to the graph of HadCRUT4 Arctic data precisely because I anticipate that you’ll call it “garbage” or “junk”. That’s what you call any temperature graph that doesn’t fit the narrative you believe in.
But I’m curious. Why does the Arctic HadCRUT4 data look almost exactly like the climate reconstructions for places like Greenland, or Alaska, or Iceland…in the Arctic region? For example:
https://notrickszone.com/wp-content/uploads/2017/02/Holocene-Cooling-Iceland-Glaciers-Temps-Fern%C3%A1ndez-Fern%C3%A1ndez-17.jpg
https://notrickszone.com/wp-content/uploads/2017/03/Holocene-Cooling-Alaska-Gulf-Wilson-17.jpg
https://notrickszone.com/wp-content/uploads/2016/12/Holocene-Cooling-Greenland-Southeast-Hasholt-16.jpg
https://notrickszone.com/wp-content/uploads/2016/12/Holocene-Cooling-Greenland-Ice-Sheet-van-As-16.jpg
https://notrickszone.com/wp-content/uploads/2016/12/Holocene-Cooling-Iceland-South-Chandler-16.jpg
And the weather and temperature variations were more extreme back in the 1920s-1940s. That high rate of variability occurred while CO2 was safely in the 310 ppm range. So what caused that, sod?
Kelly, 2016
http://www.omicsgroup.org/journals/trends-in-extreme-weather-events-since-1900–an-enduring-conundrum-for-wise-policy-advice-2167-0587-1000155.pdf
It is widely promulgated and believed that human-caused global warming comes with increases in both the intensity and frequency of extreme weather events. A survey of official weather sites and the scientific literature provides strong evidence that the first half of the 20th century had more extreme weather than the second half, when anthropogenic global warming is claimed to have been mainly responsible for observed climate change. The disconnect between real-world historical data on the 100 years’ time scale and the current predictions provides a real conundrum when any engineer tries to make a professional assessment of the real future value of any infrastructure project which aims to mitigate or adapt to climate change. What is the appropriate basis on which to make judgements when theory and data are in such disagreement?
“Why does the Arctic HadCRUT4 data look almost exactly like the climate reconstructions for places like Greenland, or Alaska, or Iceland…in the Arctic region? ”
other people have looked at that data as well. the old datasets simply are less precise than newer one (i am specifically including even satellite data in “new” data.)
“That high rate of variability occurred while CO2 was safely in the 310 ppm range. So what caused that, sod?”
i do not know. but it might be a data error.
I see. So when graphs and reconstructions of temperature rather consistently show that there was a warming during the 1920s to 1940s, a cooling between the 1940s and 1980s, and then a warming since that only matches the 1920s-’40s warmth…you claim that these data sets (HadCRUT4 instrumental, even) are “less precise” and are prone to “data error”.
sod, your “rebuttals” are getting weaker and weaker.
If you don’t like the Arctic temperature data from HadCRUT4, what data set do you prefer?
sob-sob’s LYING and deceitful MIS-INFORMATION are getting more and more DESPERATE by the day.
Really is getting to panic time for him, as his baseless AGW religion continues to crash around his feet and ears 🙂
A collations of several Iceland and Arctic temperature charts.
Enjoy, sob-sob. 🙂
https://s19.postimg.org/vws4z68s3/arctic_temp.png
https://s19.postimg.org/xn6kmx0xf/iceland.jpg
https://s19.postimg.org/djrjolyb7/iceland_since_19th__century.png
Then please respond to my post above. Further, even if the arctic situation were “dire” on what basis would you attribute such a state of affairs to CO2 emissions? What cause and effect data do you have to support such a claim?
No doubt you are right s*d. Could you please point out the reality of the situation as you see it with, perhaps, some figures or images?
I did plot sea ice thickness above:
http://psc.apl.uw.edu/wordpress/wp-content/uploads/schweiger/ice_volume/Bpiomas_plot_daily_heff.2sst.png
Arctic sea ice extend is not good:
https://nsidc.org/data/seaice_index/images/daily_images/N_iqr_timeseries.png
neither is the antarctic (which norm,ally is a favourite of “sceptics”.
https://seaice.uni-bremen.de/data/amsr2/today/extent_s_running_mean_amsr2_previous.png
Russian charts show “old ice” to be:
12% higher than 2016
41% higher than 2008
26% higher than 2009
30% higher than 2012
65% higher than 2013
MASIE shows day 125 sea ice extent above that of:
2006, 2007, 2009, 2010, 2011, 2015 and 2016
NSIDC has 2017 above 2006 and 2015 (sob LIES by not showing that) and will probably cross above 2015, 2011, and 2014 in the next day or so.
Antarctic is a SINGLE year anomaly in an otherwise rising trend, and it is above 1980 levels..
sob-sob LIES by omission, yet again.
typo correction
NSIDC has 2017 above 2006 and 2016….
“Russian charts show “old ice” to be: ”
yeah, the one source that confirms what you already know. Just ignore reality!
Only person ignoring reality here is you.
DMI, Russian, OSI all show an increase in multi-year Arctic sea ice
Masie, DMI, NDSIC show Arctic sea ice extent doing well.
NSIDC day 126 has 2017 ahead of 2004, 2006,2014, 2015, 2016.
If you are thirty years old then for the majority of your life you have been informed by the AGW consensus (of nonsense) that the Arctic ice is disappearing, however it has failed to meet its billing.
Over the last 30 years ice levels fell a few percent, before it stared rising again. It’s called NATURAL VARIATION, that’s the whole truth of the matter.
[…] Here on CO2isLife we’ve been making a couple of predictions. The first was that the record high temperatures that the climate alarmists were celebrating as proof of their theory, were, in fact, an anomaly caused by a natural phenomenon called an El Nino, and that once that natural event ended, temperatures would plummet. That is in fact what has been happening. […]
Hate to Say I Told You So, But I Told You So
Here on CO2isLife we’ve been making a couple of predictions. The first was that the record high temperatures that the climate alarmists were celebrating as proof of their theory, were, in fact, an anomaly caused by a natural phenomenon called an El Nino, and that once that natural event ended, temperatures would plummet. That is in fact what has been happening.
https://co2islife.wordpress.com/2017/05/07/hate-to-say-i-told-you-so-but-i-told-you-so/
Sure, the totally natural El Nino with the total natural El Nina drop following … what fuels those totally natural events? Why the larger than usual energy build up in recent decades?
The temperature increase (moving average) isn’t much smaller without the 3 larger El Nino spikes in recent decades … http://imgur.com/a/8Atz4
ROFLMAO.
Your moronic average USES the step change of the 1998 El Nino. The slight trend RELIES TOTALLY on that El Nino step change
Are you so moronically stupid that you can’t see that !!!
REALITY.
FFS seb.. wake up to basic mathematical analysis and for once, THINK what you are doing.
https://s19.postimg.org/v9zxq3zzn/RSS_El_Nino_step..png
I think you mean https://s19.postimg.org/v9zxq3zzn/RSS_El_Nino_step.png
Otherwise OK. Funny how that fits with the small but significant up-tick in solar activity that year.
Correlation between solar activity and El Niño Southern Oscillation (ENSO)
http://aip.scitation.org/doi/abs/10.1063/1.4930679
odd. I wonder where the extra dot came from ???
Is this what you’re saying:
– Plateau
– 1998 ENSO heat spike
– Residual heat = step change (due to ENSO, not CO2)
– Plateau
-2016/2016 El Nino = drop back to prior…
…seems like no effective step change..
Time will tell.
The series of strong solar cycles in the latter half of last century put a lot of extra energy into the system.
There is a lot of water out there, so the effect of the now sleepy sun could take a while to materialise.
The planet will be seeking a new, somewhat lower, balance point. That means losing energy from the oceans.
Let’s hope CO2 can maintain the temperature where it is 😉
[…] 3) Data Analyses Show Rapid Global Surface Cooling, Growing Arctic Ice Thickness No Tricks Zone, 6 May 2017 […]
OT.
For the last 6 days NSIDC is showing 2017 Arctic Sea Ice extent as having the SMALLEST drop from maximum this century.
Also, as of day 130, the smallest 28 day drop for the same period.