A Disgraceful Chasm Between Real-World
Observations & Climate Science Reporting

Injecting frightening scenarios into climate science reporting has seemingly become a requisite for publication.
In a new Nature Geoscience editorial, a common scare tactic is utilized by the (unidentified) author so as to grab readers’ attention.
Nature Geoscience, 2018
The East Antarctic ice sheet is currently the largest ice mass on Earth. If it melted in its entirety, global sea levels would rise by more than 50 metres.
Wow. 50 meters. That would be catastrophic.
But then we read about real-world observations for East Antarctica. And they don’t even come close to aligning with the catastrophic scenario casually tossed into the editorial.
First of all, East Antarctica is not losing mass and adding to sea levels. The ice sheet is gaining mass and thus removing water from sea levels. The surface mass gains have been occurring not only since 1800 (Thomas et al., 2017), but for the recent decade (2003-2013) too (Martín-Español et al., 2017). Even the author of the Nature Geoscience editorial acknowledges this.
Nature Geoscience, 2018
“The East Antarctic ice sheet may be gaining mass in the current, warming climate. The palaeoclimate record shows, however, that it has retreated during previous episodes of prolonged warmth.”
Not only has East Antarctica been gaining mass, the author goes on to say that it would take 100s of thousands to millions of years for Antarctica to even exhibit partial retreat. So much for the “if it melted in its entirety” warning we read earlier.
“In terms of immediate sea-level rise, it is reassuring that it seems to require prolonged periods of lasting hundreds of thousands to millions of years to induce even partial retreat.”
So if the editorial department at Nature Geoscience realizes that it would take 100s of thousands to millions of years to even witness a partial retreat of the ice sheet, is there any scientific justification for the inclusion of the sea-levels-would-rise-50-meters-if-East-Antarctica-melted commentary? Since when do imaginary scenarios pass as science?
A ‘Staggering’ 9 Trillion Tons Of Greenland’s Ice Has Been Lost Since 1900! That’s A Sea Level Contribution Of Less Than 1 Inch
It’s frightening to learn that the Greenland Ice Sheet has lost a “staggering” 9 trillion tons of ice since 1900, which is what the Washington Post warned us about in 2015.
It’s not frightening to learn that 9 trillion tons of ice losses actually amounts to less than 1 inch of sea level rise contribution from Greenland meltwater in 115 years.
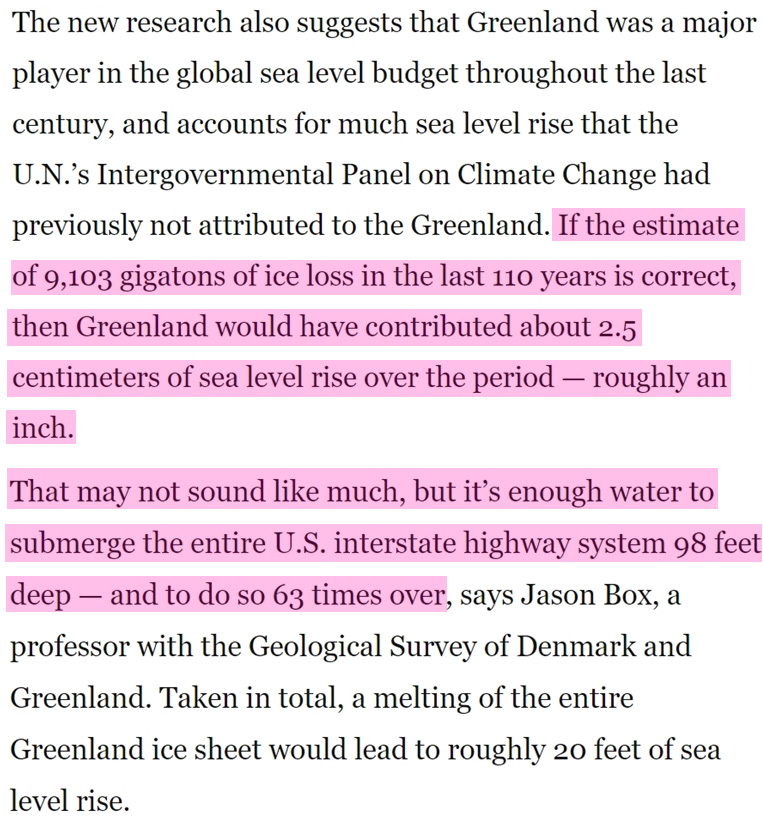
Since a total sea level rise contribution of 1 inch in 115 years from the Greenland ice sheet isn’t scary, the author of the Washington Post article (Chris Mooney) finds it necessary to offer his readers a macabre thought experiment: What if that additional 1 inch of water sitting atop the world ocean were to be collected somehow and then dumped onto all the United States interstate highways? Now that would be scary. It would mean that 1 inch of sea level rise turned into 98 feet of sea levels rise (63 times over) in very same imaginary world where additional sea water is dumped onto U.S. interstate highways.
This is how the modern version of climate science works.
Below are a few more examples of glacier melt and sea level rise observations from recently-published papers casting doubt on the tragic, alarmist, and attention-seeking headlines that are so prevalent today.
1. ‘Pine Island Glacier Is The Largest Current Antarctic Contributor To Sea Level Rise’ – But Has ‘Not Shown Any Clear Trend Over 68 Years’ (1947-2015)
Arndt et al., 2018
“Pine Island Glacier is the largest current Antarctic contributor to sea level rise. Its ice loss has substantially increased over the last 25 years through thinning, acceleration and grounding line retreat. However, the calving line positions of the stabilizing ice shelf did not show any trend within the observational record (last 70 years) until calving in 2015 led to unprecedented retreat and changed alignment of the calving front. … Despite the thinning and flow acceleration of PIG [Pine Island Glacier], and sustained, rapid thinning of the ice shelf over at least the past 25 years the position of the ice front had not shown any clear trend over 68 years of observations prior to 2015 (Bindschadler, 2002;MacGregor et al., 2012;Rignot, 2002).”
2. More Land Area Above Sea Level In 2014 Than In 1971 In The Tropical Pacific
Kench et al., 2018
“We specifically examine spatial differences in island behaviour, of all 101 islands in Tuvalu, over the past four decades (1971–2014), a period in which local sea level has risen at twice the global average (Supplementary Note 2). Surprisingly, we show that all islands have changed and that the dominant mode of change has been island expansion, which has increased the land area of the nation. … Using remotely sensed data, change is analysed over the past four decades, a period when local sea level has risen at twice the global average [<2 mm/yr-1] (~3.90 ± 0.4 mm.yr−1). Results highlight a net increase in land area in Tuvalu of 73.5 ha (2.9%), despite sea-level rise, and land area increase in eight of nine atolls.”
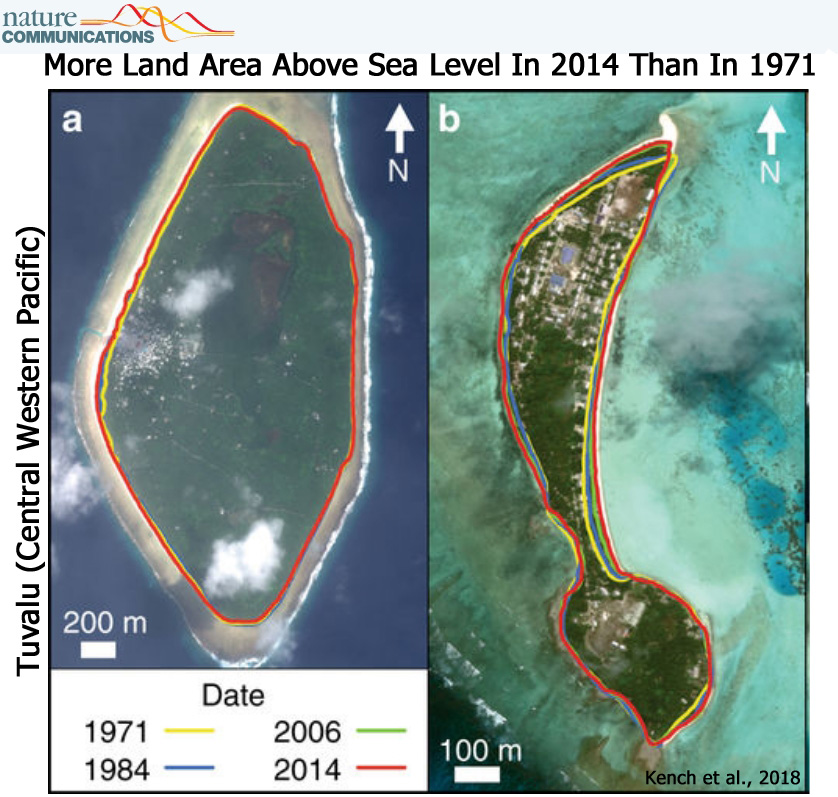
3. More Land Area Above Sea Level In 2015 Than In 1985 For The Entire Globe
Donchyts et al., 2016
“Earth’s surface water change over the past 30 years [1985-2015] … Earth’s surface gained 115,000 km2 of water and 173,000 km2 of land over the past 30 years, including 20,135 km2 of water and 33,700 km2 of land in coastal areas.”
(press release)
Coastal areas were also analysed, and to the scientists’ surprise, coastlines had gained more land – 33,700 sq km (13,000 sq miles) – than they had been lost to water (20,100 sq km or 7,800 sq miles).
“We expected that the coast would start to retreat due to sea level rise, but the most surprising thing is that the coasts are growing all over the world,” said Dr Baart. “We were able to create more land than sea level rise was taking.”
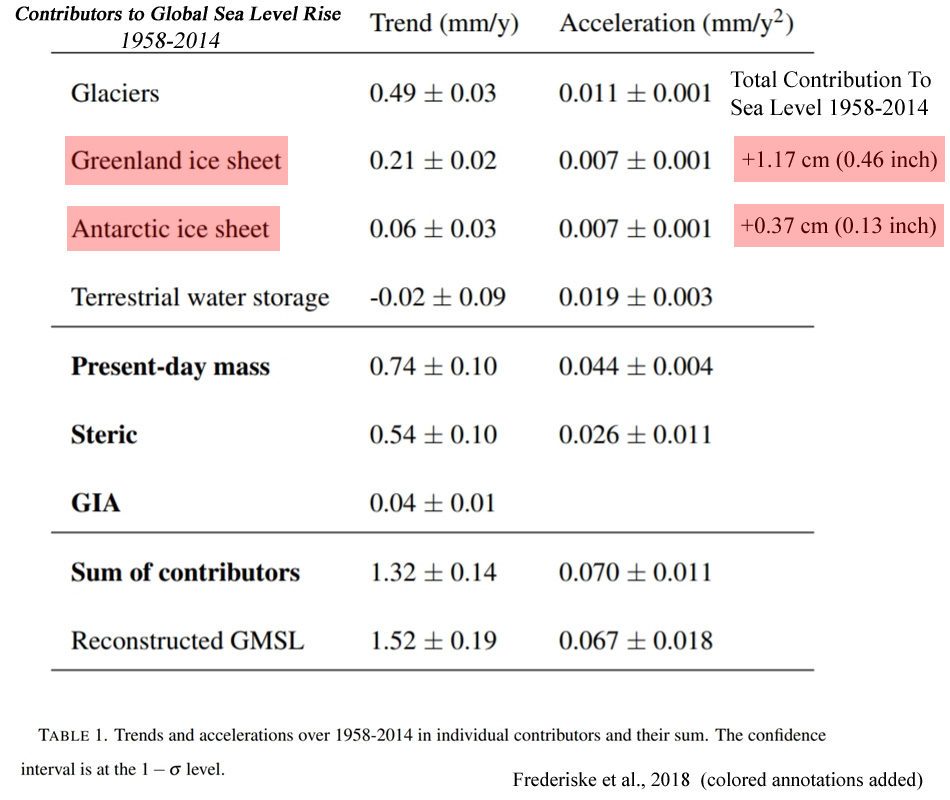
4. Greenland And Antarctica Combined Contributed A Total Of 0.59 Of An Inch To Sea Level Rise Between 1958-2014
Frederiske et al.,2018
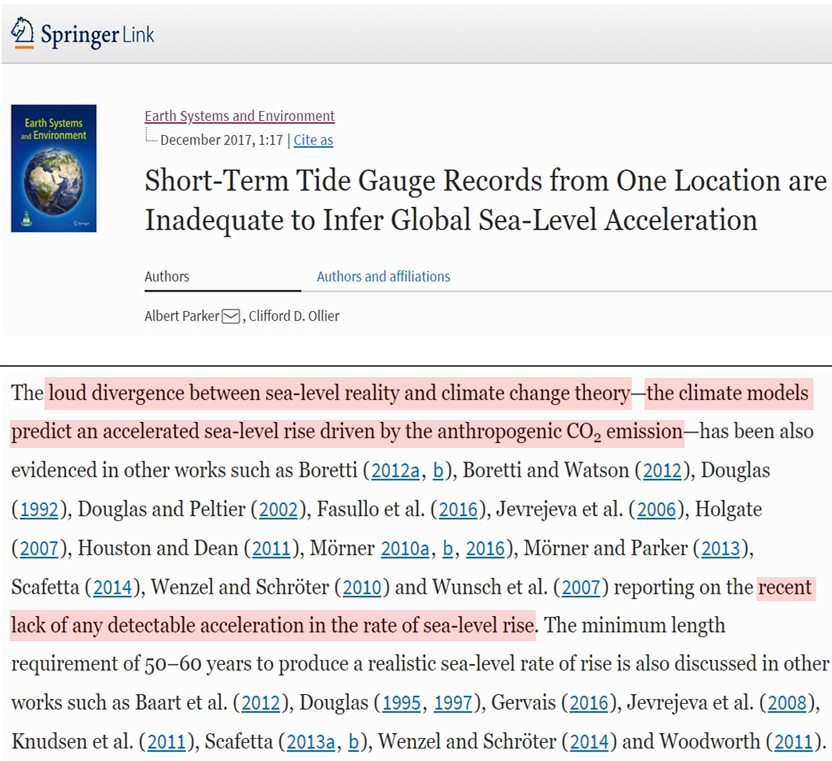
5. ‘Recent Lack Of Any Detectable Acceleration In The Rate Of Sea-Level Rise’
Parker and Ollier, 2017
“The loud divergence between sea-level reality and climate change theory—the climate models predict an accelerated sea-level rise driven by the anthropogenic CO2 emission—has been also evidenced in other works such as Boretti (2012a, b), Boretti and Watson (2012), Douglas (1992), Douglas and Peltier (2002), Fasullo et al. (2016), Jevrejeva et al. (2006), Holgate (2007), Houston and Dean (2011), Mörner 2010a, b, 2016), Mörner and Parker (2013), Scafetta (2014), Wenzel and Schröter (2010) and Wunsch et al. (2007) reporting on the recent lack of any detectable acceleration in the rate of sea-level rise. The minimum length requirement of 50–60 years to produce a realistic sea-level rate of rise is also discussed in other works such as Baart et al. (2012), Douglas (1995, 1997), Gervais (2016), Jevrejeva et al. (2008), Knudsen et al. (2011), Scafetta (2013a, b), Wenzel and Schröter (2014) and Woodworth (2011).”
“[T]he information from the tide gauges of the USA and the rest of the world when considered globally and over time windows of not less than 80 years […] does not support the notion of rapidly changing mass of ice in Greenland and Antarctica as claimed by Davis and Vinogradova (2017). The sea levels have been oscillating about a nearly perfectly linear trend since the start of the twentieth century with no sign of acceleration. There are only different phases of some oscillations moving from one location to another that do not represent any global acceleration.”
“The global sea-level acceleration is therefore in the order of + 0.002 ± 0.003 mm/year², i.e. + 2 ÷ 3 μm/year², well below the accuracy of the estimation.”





Unfortunately this alarmist screaming comes as no surprise.
And the screaming will get louder as more evidence for climate change having little effect mounts up and the grants dry up and the gravy-train slows.
I would be very skeptical of that happening … if I were a skeptic 😉
“I would be very skeptical of that happening … if I were a skeptic”
Says the very same person who literally believes that climate change is causing 30,000 species a year to go extinct…even though only 1 species has been confirmed to have gone extinct since 2000 (a mollusc), and that ocean “acidification” is happening so fast that marine species cannot adapt.
https://notrickszone.com/2017/10/16/recent-co2-climate-sensitivity-estimates-continue-trending-towards-zero/#comment-1232607
SebastianH: “Regarding extinction of species, why do you think 30,000 species lost per year is a big number? We are already at or over that rate.”
https://notrickszone.com/2018/01/04/485-scientific-papers-published-in-2017-support-a-skeptical-position-on-climate-alarm/#comment-1246210
SebastianH: “They [marine species] might be able to adapt, but not at the speed acidification is happening.”
Why should we assume that your alarmist beliefs are accurate, SebastianH? Why shouldn’t we be skeptical of them?
@ Kenneth
SebH claims that ocean pH changing too rapidly for seafood to adapt.
hahahahahaha
This one never gets old.
https://sanctuarysimon.org/regional_docs/monitoring_projects/100240_167.pdf
pH goes up and down repeatedly from about 7.75 to 8.15, with not the slightest hint of any long term trend.
NTZ readers can believe real world data, or the outlandish claims of some anonymous activist chatbot troll who gets his information from brainwashed researchers who would be out of jobs if they dared to deviate from the warmist narrative.
Believe real world data then:
http://ocean.si.edu/ocean-acidification (http://ocean.si.edu/sites/default/files/styles/colorbox_full_width/public/photos/hitimeseries.jpg)
http://www.iupui.edu/~g115/mod07/casestudy01.html
http://www.azimuthproject.org/azimuth/show/Ocean+acidification
Dear old Aunty (ABC) got on the band wagon as well, but are her numbers out by a factor of 10?
http://www.abc.net.au/news/science/2018-02-13/25-years-of-satellite-data-confirms-global-sea-level-rise-rate/9416570
Seb ,
First link: NO DATA, just empty ranting a-la-la seb… Consign to bin.
2nd link, cites Wiki many times.. not accepted in ANY science paper. Consign to bin.
3rd link. Those shells ere shown to be uninhabited for ages, of course they break down, always have always will. You do know that shell creatures adjust the pH towards acidic to aid building their shells, don’t you?
Or are you IGNORANT of that as well.
Consign to bin.
4th link: that pic “Here is a diagram that shows the changes in ocean acidity from pre-industrial times up to 2000:” has to be the biggest laugh out !!
They can’t measure pH that accurately now, let alone pre-industrial. How did that EVER get through any review, even pal-review !!!
Consign paper to bin.
Recent measurements over a very short period during changes to PDO. ZERO PROOF that CO2 caused it, just mindless correlation and models.. Consign paper to bin.. again..
You really have to be more sceptical of the JUNK they feed you, seb, your mind will get fat and lazy and will atrophy even further, if that is even possible..
4th paper.
a LIE in the very first line.
“it is making the oceans more acidic”
This is NOTHING but baseless, anti-science propaganda papa.
Ocean waters are NOT acidic, they will NEVER become acidic.
CONSIGN TO BIN.
And the experiment of “aerating” water with CO2, giving no time to adapt, is yet again a MONUMENTAL FAILURE of any scientific procedure.
Consign to SEWER. !!
What a perfect reply for an insane climate change denier …
Yes, I was aimed at you, ..
… because we all KNOW you have ZERO COMPREHENSION of science, and are in CONSTANT DENIAL of all data and physics of climate.
And yes, you really are […], seb.
I don’t know, Andy. I mean, if Steve (tie dye) Esterbrook
http://www.azimuthproject.org/azimuth/show/Steve+Easterbrook
says it’s so, it must be so. After all, would a comp sci prof, and ocean fantasy modeler extraordinaire, mislead us?! //sarc//
Indeed Kenneth,
And of course there’s the cAGW loudly promulgated nonsense about the tropical tropospheric hot-spot that never appeared, never could appear (it’s based computer modeled nonsense).
Such was the embarrassment by the cAGW activists that they concocted an even more unlikely (and laughable) reason for why it(the hot-spot) did not appear, releasing on the world even more flights of fantasy.
When will they learn — when in a hole stop digging.
“When will they learn — when in a hole stop digging.”
seb just keeps digging more and more manically, as the slimy ooze he shovels keeps pouring back in on him. !!
Its hilarious to watch. 🙂
Well, I’ll reply with a quote from a much loved website in skeptic denialist circles: https://www.skepticalscience.com/tropospheric-hot-spot-advanced.htm
A great deal of the confusion surrounding the issue of temperature trends in the upper troposphere comes from the mistaken belief that the presence or lack of amplification of surface warming in the upper troposphere has some bearing on the attribution of global warming to man-made causes.
It does not.
But of course, explanations from brainwashed researchers isn’t any good. You have to rely on conspiracy theorists and hoax papers … so impressive 😉
SkS are probably in even deeper DENIAL that you are, seb
They have to DENY that the Hot Spot was prediction.
because THEY KNOW IT DOESN’T EXIST.
because they KNOW that there is no science backing the LIE of CO2 warming.
Do you have any actual science to back up the AGW LIES about CO2?
We have never seen any from you.
We have been waiting a LONG, LONG TIME.
And quoting SkS.. roflmao..no wonder you have EMPTY anti-knowledge as your only support.
That is not what I said … you even quote what I said and that is your interpretation? Why are you making this up? What I said was what you quote.
BTW, here is a new study about extinction rates: http://science.sciencemag.org/content/348/6234/571
Oh please, you still think that acidification is no problem? Pick one: https://scholar.google.de/scholar?q=acidification+coral+reefs
You should be skeptical about everything. So far you have shown a tendency to believe any bullcrap as long as it feels like it somehow “supports a skeptical view point”. That is not skeptical, that is just sad. You are living in denial.
What you said, word for word: “Regarding extinction of species, why do you think 30,000 species lost per year is a big number? We are already at or over that rate.”
If we “are already at or over” the rate of 30,000 species extinctions per year, how does this not mean that you believe that “we are already at or over that rate” (30,000 extinctions per year)? What is the correct interpretation that you have imagined for that quote?
How is it different to say that you believe 30,000 species a year are “already” going extinct when that’s what you wrote? There has been only 1 species that has been confirmed to have gone extinct since 2000. That’s a rate of about 0.6 species per decade. Between 1500 and 2000, 800 species went extinct (16 per decade), nearly all during the Little Ice Age and on islands. In other words, climate change has dramatically lowered the extinction rate (if we rely on the assumption that climate determines extinctions).
http://www.bbc.com/news/magazine-17826898
“It is possible to count the number of species known to be extinct. The International Union for Conservation of Nature (IUCN) does just that. It has listed 801 animal and plant species (mostly animal) known to have gone extinct since 1500. According to IUCN data, for example, only one animal has been definitely identified as having gone extinct since 2000. It was a mollusc.”
Uh, SebastianH, that paper isn’t about extinction rates that are already occurring. It’s a prediction paper, based upon models, for how many extinctions that may possibly might perhaps one day occur due to climate change. That’s why it says it’s about “…how species might respond to our changing climate”.
That’s neither what you wrote or what I identified as what you wrote. (And you know that. This is just another of your made-up arguments.) It is your claim that the rate of acidification (i.e., pH lowering) since the beginning of the anthropogenic influence is so fast that marine species cannot adapt to it. The problem is, no clearly identifiable trend is detectable. Scientists claim that the rate trend of pH lowering in the last 200 years has amounted to ~0.00004 per year, which is below the uncertainty range. And even if we assume it’s accurate, when we consider that pH naturally rises and falls by about +/-0.5 over the course of a single decade, this means that natural changes in seawater pH occur at rates 100s of times faster than the trend attributed to anthropogenic CO2. You have been invited several times to support your beliefs that the trend attributed to anthropogenic influences is “too fast” for marine species to adapt to. You cannot do so, obviously. For the basics in ocean “acidication” education, please read this summary article replete with a few dozen references:
The ‘Ocean Acidification’ Narrative Collapses Under The Weight Of New Scientific Evidence
—
McElhany, 2017
https://academic.oup.com/icesjms/article-lookup/doi/10.1093/icesjms/fsw085
“Documenting an effect of OA [ocean acidification] involves showing a change in a species (e.g. population abundance or distribution) as a consequence of anthropogenic changes in marine carbonate chemistry. To date, there have been no unambiguous demonstrations of a population level effect of anthropogenic OA [ocean acidification], as that term is defined by the IPCC. … [I]t is important to acknowledge that there are no studies that directly demonstrate modern day effects of OA [ocean acidification] on marine species.”
—
So I am “living in denial” when I don’t agree with you that 30,000 species per year are going extinct? That the Earth is browning and deserts are expanding according to satellite data (another of your unsupported claims/beliefs)? That the pH lowering “trend” over the last 200 years is too fast for marine species to adapt to? What, specifically, is the “truth” that I am denying?
“You should be skeptical about everything.”
Yet you are sceptical of none of the BS that your AGW masters feed you, even though you are totally EMPTY of any sort of science, or physics to back up one single piece of the scam religion
You remain EMPTY seb.
And in deep DENIAL of the facts.
Not “Says the very same person who literally believes that climate change is causing 30,000 species a year to go extinct”
And then you do this … of course you think acidification is not a problem when you argue that species have no problem adapting to it at the rate it is happening. The one making up arguments is you, Kenneth. All the time! And you don’t even recognize it anymore because you are too busy finding cherry picked quotes.
It’s a meta-analysis of 131 published studies. Do you think those studies are basing their predictions on imagination or is it rather more likely that they are extrapolating past acceleration in extinction rates (google “background extinction rate”)? Maybe you should just read them and not make up some nonsense.
Only if you are imaging my replies never existed.
Yeah, we all know what you consider scientific evidence. Your card house of phony papers, supporting nonsense and creative interpretation of what people actually say/write is collapsing. That’s all.
You are living in denial because
Just as I wrote … you grasp at anything that remotely sounds like it could support your belief, not being skeptical about it at all.
It’s like the anti-vaxxers and flat-earthers … I am sure they think they have very good “scientific” arguments too and everyone telling them otherwise is just making up unsupportable stuff. You are even more in denial if you don’t recognize the similarities.
What is the correct interpretation that you have imagined for that quote?
Oh please, SebastianH — Don’t leave us in suspense any longer. For the 3rd time now, if your quote does NOT mean what I wrote, very specifically identify what that quote means. Here it is again:
SebastianH: “Regarding extinction of species, why do you think 30,000 species lost per year is a big number? We are already at or over that rate.”
If that quote does NOT mean that you think we “are already at or over” the 30,000 species lost per year rate due to climate change, what exactly does it mean? I am waiting for your imaginative re-interpretation of what “we are already at or over” the rate of 30,000 species lost per year really means. And yet when I ask you for clarification, you just write that it’s not what you wrote.
And at what rate is ocean acidification happening, SebastianH?! The natural pH variability is +/- 0.5 within a matter of a decade. What’s the 200-year trend that is assumed to be attributed to anthropogenic CO2 rise? Would you agree that the 200-year trend is hundreds of times less rapid than the natural, year-to-year variation? If so, why would the anthropogenic 200-year trend be deleterious, but the natural variation that is 100s of times more rapid be innocuous? Explain this circular logic of yours, SebastianH. Why are you continuing to pretend that you don’t know that this has been what I have been arguing?
As I have pointed out already, they’re basing their predictions on models, not observations. According to real-world observations, we had 16 species losses per decade during 1500 to 2000 C.E. We’ve had 0.6 species lost per decade since 2000. What would the reason be for this dramatic slowdown in species losses if the extinction rate is determined by global warming? We’re modeled to get over a million species lost by 2050 (which is 30,000+ per year) according to Thomas et al. (2004). If real-world observations don’t match the models forecasting catastrophic species loss, why do you nonetheless side with models anyway? Why not base your beliefs on real-world observations instead of catastrophic modeling predicated on anthropogenic CO2 emissions? Rhetorical question, of course. Quite simply, you’re no skeptic, but a believer in catastrophic anthropogenic global warming. That’s why.
What acceleration in extinction rates? The vast majority (well over 90%) of the 801 species that have gone extinct since 1500 were lost prior to 1950. There has been a rapid and dramatic deceleration in the extinction of species since anthropogenic emissions began rising in the 1940s. In other words, the exact opposite of your catastrophic beliefs has occurred…and in the real world. Not models. Observations.
You have been invited several times to support your beliefs that the trend attributed to anthropogenic influences is “too fast” for marine species to adapt to. You cannot do so, obviously.
YOUR REPLIES HAVE NEVER ANSWERED THIS SPECIFIC QUESTION! You just make up your own positions, attribute them to me, and then feign answering the question you know I didn’t ask!
You’ve also never answered my questions as to what satellite data you have found that says the Earth is browning and deserts are expanding because of CO2. Remember this?
Desertification[?] [S]atellites show the opposite happening [greening].
Provide the satellite evidence (which you claim is all you can find) that says the Earth is browning. Stop evading.
So the papers are phony, huh? Are the scientists who write them and who are directly quoted phony too? Please identify the phony papers and scientists in that article.
I assume you have no idea that the vast majority of those who read this blog and who view your posts are likely to conclude the very same things about you that you are accusing me of here. I find it rather sad that you’ve been reduced to name-calling again.
“if I were a skeptic”
But you aren’..
You are a RABID AGW sympathiser who is totally unable to see that there is very little proof of CO2 warming anything (if there was you would have produced it by now)
.. and an ever growing amount of REAL data showing that CO2 has ZERO to NONE effect on warming anything
You are a DENIER, seb, through and through..
.. a DENIER of real science and real data.
You got that wrong. There is no real “climate debate”. It’s just science on the one side and on the other side denial. I hope you guys will go through the stages of denial quick enough to realize that you are wasting your energy on a futile cause.
It’s funny that you call me a denier now. You, the one who thinks that a chair performs work holding up a weight. You, the one who thinks the evaporation increase from an increasing OHC overcompensates it. Sorry, get a good physics book or go surfing. You aren’t any good at this physics thing …
“It’s funny that you call me a denier now.’
YOU are the one DENYING facts and real DATA
You are the on TOTALLY UNABLE to support the very basis of your wacky AGW religion.
You are the one SO WILFULLY IGNORANT that you cannot grasps basic concepts of structural mechanics… they are obviously WAY BEYOND you.
Anyone can look up “strain energy” and see that it is exactly what I described it as…
… still.. it will always remain WAY beyond you.
You are in DEEP WILFUL DENIAL, because excepting the FACTS would destroy you mentally, even more than your brain-washed mush is currently scrambled.
I suggest you look up what strain energy is my friend. Any idea what “undergoing deformation” means? Sit on a chair, it undergoes deformation exactly once. That’s the strain energy stored in the chair. Any warming from that dissipates to the environment. No work is performed to hold you up on that chair.
Maybe it becomes clearer to you when I ask you to provide the resulting strain energy from sitting on a chair for 1 go r vs. 2 hours. Let’s see you calculating the result. Or will you evade because you know it’s the same value?
STRAIN ENERGY of the member is defined as the INTERNAL WORK DONE in deforming the body by the action of externally applied forces.
Learn, or REMAIN FOREVER IGNORANT, seb
http://www.nptel.ac.in/courses/112107146/lects%20&%20picts/image/lect38/lecture38.htm
poor seb, living in DEEP DENIAL at the bottom of a slimy troll-hole. And feeling totally at home.
Poor seb, you have NEVER done even the simplest course of structural mechanics have you.
ZERO KNOWLEDGE.
ZERO COMPREHENSION.
ZERO UNDERSTANDING.
Just yap mindlessly.
While ever that strain energy exists under a load, internal work is being done.
Well Seb you need to be a skeptic because the very role of a scientist is to be skeptical.
We also have to be honest with ourselves.
I think you are basically a shit stirrer.
“basically a shit stirrer”
His only role in life…
… and all he ever aims to be.
Go then Seb. Show me one, just one, proven, not “maybe”, or “the models project” negative effect of climate change.
And while you are at it please comment on the proven benefit of increased net primary productivity. Some 15 to 20% over the last 15 years.
That’s more food for us and wildlife.
SebastianH says he can only find satellite data that show the Earth is browning and deserts are expanding. And yet when asked to produce this data (that he claims to have found), he refuses to do so. It’s as if he just made it up.
Good job you are not scientist, then, as scepticism is an ESSENTIAL element of scientific rigour.
(Dang! I hadn’t noticed that replies are not comment-specific – that retort was aimed at SebastianH, whoever he/she might be.)
The problem, as I have come to see it, is that for believers in the warmist cult; reality isn’t supported by their theories or the data that’s adjusted to fit them.
Home Test.
Put an ice cube in a glass of water. Level rises.
Cube melts.
No change to previously raised water level.
It’s even more fun if you use fairly strong brine instead of water. 😀
It’s even more fun if you use single-malt scotch… though it can be difficult stopping the level falling too fast before the experiment is over.
Well, thank you for explaining that floating ice that melts doesn’t contribute to sea level rise. You have discovered a basic law of physics, congratulations.
Now put an ice cube in an empty glass and watch it melt. Level rises, but some here would say that evaporation caused by downwelling IR radiation actually causes cooling. So, in this new world of physics the water will evaporate and if we are lucky an ice cube forms itself if we hit that glass with IR light 😉 Isn’t that fun?
SebH not good physics. radiation always cooling. Is sending energy away! Water evaporating always cooling. Its need energy for evaporation.
SebH has not think!
Of course it is cooling, what do you think I am saying? But you guys can’t be possibly thinking that a warmer surface that evaporates more, is actually colder than a colder surface that evaporates less. Are you?
SebH not clear. Warming cooling same time. How now decide warm or cold. Best is do sum energy. It same no different. only when water evaporate no temperature change. Make no sense talking warmer or colder. it different process.
Seb, your total LACK of any sort of comprehension of basic physics and MEASURED science, is really quite TROL-LIKE.
Nobody, I repeat NOBODY could possible be as DIM-WITTED as you are making yourself out to be
You are in TOTAL WILFUL DENIAL and PEPETUATE INGORANCE of all science, physics, and the mechanics that builds the world.
PERPETUAL IGNORANCE, not perpetuate…….
Darn eyes !!
Do you think that writing in caps lock with colorful insults is a convincing method to transport you wastly superior knowledge to the interested reader? 🙂
That’s odd. When I put ice in a glass full of liquid the level always falls. If I wait till after the ice melts, my drink won’t be cold anymore. 😁
Seb, even the most unobservant child knows that evaporation cause cooling.
There are whole industries built around this fact.
Just because you can’t prove otherwise (EMPTY as always), and are left with NOTHING but making childish anti-science comments, doesn’t change that fact !!
Even cows know that when it’s hot out, if they lie down on wet ground they’ll cool off. Conclusion = cows are smarter than warmists.
I’m afraid this is a non sequitur, yonason. (o:
No it’s not, Kenneth. It’s a punchline. 🙃
OK, so my comedic timing may be a bit off…
Seriously, cows do that.
http://extension.uga.edu/publications/detail.html?number=B1426
It’s less about evaporation than about specific heat, though the moisture on their hides WILL act like sweat, as well.
My point being that warmists have less of a clue of how nature works than dumb animals do.
And that’s the memo.
(I’m fed up with the chatbot’s, or can you tell?)
Dogs pant, using evaporation to COOL themselves.
Even a mindless Chihuahua would know this.
But seb doesn’t. !!
Whole industries are built around the laws of physics.
Again, you have two cups of water with identical heat content and identical surroundings. You want the second cup of water to evaporate more, what do you have to do to its temperature? Will that cup then be cooler or warmer than the other cup?
It’s not that hard a question, yet you avoid answering it every time. Why?
“Whole industries are built around the laws of physics.”
Not your laws of fantasy fizzics, that is for sure.
Oceans are not cups, seb.
You cannot just heat the surface of the water in a cup. It is a NONSENSE brain-fart on your behalf, seb. As always.
Your grip on logic and science seems to be basically NON-EXISTANT.
Stop your irrelevant analogies and try working with facts and data and measurement, and try to stay on the actual topic for a change.
Provide some empirical data that shows that increasing the CO2 above a body of water increases it temperature
If you have two cups containing the same volume of water and with the same heat content, and you wish to make an observation of a passive situation, then changing the temperature of either negates your experiment. The only way you could increase the evaporation of one over the other would be to change either the surface area and/or the air-flow over the surface; which is why wide cups cool faster than tall mugs, and why people blow over their cup.
And then there are the industries built on getting rich from goveryhandouts and bilking the public.
https://www.wind-watch.org/news/2017/09/20/wind-energy-scam/
Like all the other con men, SebH invokes “the laws of physics” to pretend there is any justification for such monumental waste.
“government handouts”
More on the wind “power” scam.
http://www.epaw.org/echoes.php?lang=en&article=n612
“Level rises, ”
Not while the ice is melting, seb.
Even you know that, don’t you ???
Sorry you still can’t grasp the idea of latent heat and the fact that evaporation has been MEASURED in actual empirical science, to cause a slight cooling of the top 1mm.
But empirical science and real measurements mean ABSOLUTELY NOTHING in your little fantasy fizzucs world, do they.
You even think that a chair supports you without doing anything. Quite bizzare, totally ignorant, and totally against all known and validated structural mechanics.
And you have shown that you are INCAPABLE of ever knowing, because you have made it very clear that you wish to remain forever, WILFULLY IGNORANT.
Melting ice that sits on the ground always causes a rise in the water level.
A chair gets compressed by me sitting down on it exactly once. It doesn’t perform any work supporting my weight. Claiming that is nonsense and either you are trolling people pretending that or you should really take a physics lesson at your local highschool …
“Melting ice that sits on the ground always causes a rise in the water level.”
You said put it in a glass of water.
Try to keep you LIES straight, seb
Still the manic DENIAL of basic structural physics, that ANYONE can verify just by looking it up.
http://www.nptel.ac.in/courses/112107146/lects%20&%20picts/image/lect38/lecture38.htm
REMAIN forever ignorant, seb. It is WHO YOU ARE.
Stick to your junior high physics fail, seb.
So sad, so pathetic.. so seb.
On top of that physics book you should read, maybe reading glasses are a good investment too.
I wrote: “put an ice cube in an empty glass“.
Exactly! And how do you get the impression that the deformation is an ongoing process?
Again, please tell us how much internal work is done (by the chair) when sitting on a chair for 1 hour vs. 2 hours? It’s really not that hard a problem to solve.
Poor seb, still incapable of basic comprehension
While ever that strain energy exists, there is work being done.
I know basic concepts are an anathema to you, but do try to learn at least the very basics of structural mechanics.
Or just remain your ALWAYS ignorant self.
We get the message, Andy. No need to keep repeating yourself. We are fully aware of what you think of Seb’s smarts and knowledge.
“We are fully aware “
I know we are all fully aware…
…but Seb needs to realise just how limited his knowledge really is.
Not just limited, but more like anti-knowledge.
I’m just trying to help him. !! 🙂
To fix his problems, he has to first accept that he has a MAJOR knowledge deficit problem in basically every field he tries to discuss.
What SI derived unit is kg.m²/sec ?
This is what you end up in if you multiply ‘work’ x ‘time’
“on a chair for 1 hour vs. 2 hours”
Seb, the units of strain energy are already those of WORK.
Are you proposing we invent a new SI derived unit, just to suit your NO-SENSE question?
If the global average temperature had to fall by 3deg C at least one billion humans will die of the cold, hunger and disease.
But they wouldn’t have to die, if the technological and financial resources were in place to deal with the problem. Unfortunately, greedy scammers are preventing development of useful technology, and depleting those resources in pursuit of fake solutions to a fake problem. And they do that in order, as they claim, to make the world colder (as if they could). Warmists are not good people.
Wow, that level of conspiracy thinking is amazing.
P.S.: It’s not to make the world colder, it is to limit global warming. If we are lucky, we can do that in this century.
I’ve got your TWILIGHT ZONE “conspiracy thinking” right here, seb.
https://www.smithsonianmag.com/science-nature/reality-hotter-world-already-here-180951172/
In other words, “Be afraid. Be VERY afraid.”
https://youtu.be/EKCpB7aAPvw?t=2
The warmunistas say it’s hotter than ever, and CO2 is the cause.
They want to lower our output of CO2 on the unverified presumption that will reduce atmospheric [CO2].
If they are correct, the result of reducing CO2 emissions will be that the temperature MUST fall.
What part of “they want temperatures to fall” doesn’t follow logically from that?
Wow, “the unverified presumption”. Today you are in top form Yonason. Reducing Co2 emissions will not lead to lower temperatures for a long time. The concentration has to come down first, then it has to get to a level where the forcing levels out, and then we have oceans with a lot of stored energy to support warmer temperatures for quite some time.
It will take ages until effects of reducing CO2 emissions will be felt. It will also take ages until the results from our current emissions manifest. You skeptics seem to think that there is a 1:1 correlation between GHG concentration and temperature. That’s not the case, there is a lag.
Can you pinpoint/cite the observational evidence from real-world data that supports this? Because this sounds entirely hypothetical and made up. The paleoclimate data do not support this. The CO2 concentration rise follows warming within a few hundred years. The CO2 concentration decline takes thousands of years to draw down after the temperature has declined.
What is that forcing leveling out value, exactly? Do you have scientific data to back up this claim, or is this just assumptive too?
Why should we believe you know what you’re talking about with what will happen decades and centuries from now when even the IPCC acknowledges that 114 of 117 climate model simulations couldn’t even get the 1993-2013 temperature trend right—they were wrong by more than a factor of two?
How long do you suppose these “ages” might last? Because according to climate modelers on your side, the strongest impact of our current emissions takes only 10 years on average to manifest themselves. 10 years. Can I assume this is brand new information for you…since your claim is that it takes “ages” according to modeled assumptions?
—
http://iopscience.iop.org/1748-9326/9/12/124002/article
“It is known that carbon dioxide emissions cause the Earth to warm, but no previous study has focused on examining how long it takes to reach maximum warming following a particular CO2 emission. Using conjoined results of carbon-cycle and physical-climate model intercomparison projects, we find the median time between an emission and maximum warming is 10.1 years.”
“Reducing Co2 emissions will not lead to lower temperatures for a long time.”
Reducing CO2 won’t have any effect on temperatures at all.
There is NO EVIDENCE that enhanced atmospheric CO2 causes any warming what-so-ever.
There is no reason to assume holding it steady or reducing it (to the detriment of the whole biosphere) would have any effect on temperature either.
This whole CO2 nonsense is a load of anti-science BS !!
The ONLY thing CO2 does is ENHANCE both the land and ocean biospheres.
ALL animals and plants benefit from raised CO2 at any level the atmosphere could ever possibly attain..
“That’s not the case, there is a lag.”
Yes, CO2 LAGS temperature at all time scales.
If CO2 caused any warming, you would produce the evidence, but you NEVER had.
You have proven that you are TOTALLY INCAPABLE of producing any science to support the CO2 fallacy.
You are EMPTY… always.
“It will take ages until effects of reducing CO2 emissions will be felt. “
Yep, especially since CO2 emission level will just keep climbing and climbing, probably for at least the next century as country after country realise that fossil fuels are the best and cheapest way to build themselves out of third world status.
1600 new coal fuelled power stations around the world. Will all last at least 50 years each.
Fossil fuels still 80%+ of total energy use for MANY, MANY years to come.
You and your pathetic religious and stupid anti-human, anti-development anti-CO2 Agenda have FAILED UTTERLY, seb
Get used to it 🙂
You do know that the current CO2 concentration increase is man made, do you? Or are you denying that? The way you ask these questions implies that.
Of course CO2 concentration also follows temperature up and down. That follows from the laws of physics (the oceans being either sink or source depending on temperature and partial CO2 pressure). However, if something introduces extra CO2 in the cycle, it obviously departs somewhat from that connection. But I suppose that is not really happening in your world, right?
That depends on what is going to happen. Currently we are experiencing GHG forcing. It will continue to be a forcing until equilibrium is reached again. That “leveling out value” happens when the ECS temperature is reached.
You shouldn’t, you should be very skeptical about anything you read on the internet, even “scientific” papers and especially “blog science”. You should also not fall so easily for scientific nonsense and only read into papers what you want to believe. You claim to be skeptic, but you are only skeptic about certain things and blindly believe things supporting that skepticism. Don’t you recognize that cognitive dissonance?
Don’t believe BS and don’t make opponents do homework for you. Find out what they are talking about with an open mind.
I wish you would take all sentences you read as literally as that one about the manifestation of the effect by me. I am sorry that it wasn’t clear enough that “current emissions” is for me an ongoing thing. We will not be able to stop emitting CO2 tomorrow.
You can assume what you want, as you always do.
@AndyG55: I’ll stop replying to you and you stop posting nonsense, deal?
“You do know that the current CO2 concentration increase is man made, do you?”
Partially, (best science says around 15%). And HIGHLY BENEFICIAL.
Apart from that , your whole post is just another load of self-opinionated garbage, .
CO2 emissions will continue to rise for the foreseeable future.
There is ZERO evidence that enhanced atmospheric CO2 is in any way a problem and MUCH evidence that it is ENTIRELY BENEFICIAL.
So stop posting your brain-washed ranting, seb, and produce some actual scientific evidence to back up your wacky little fantasies.
Your posts remain , as always, TOTALLY EMPTY of anything but mindless rhetoric and BS.
SebH tries to feed us the IPCC talking point that CO2 effects won’t go away in like forever. Problem is, the IPCC bases it’s conclusions on assumptions that dramatically deviate from virtually everyone else.
http://jennifermarohasy.com//wp-content/uploads/2009/09/Carbon-dioxide-residence-time.jpg
But we’re supposed to be “the deniers?”
Sure, they have their opinion, but that doesn’t make it true. One must keep in mind that extraordinary claims require extraordinary proofs. I’m still waiting to say theirs.
See also Murry Salby’s material on why human contributions to climate change may well be minimal.
http://edberry.com/blog/category/authors-climate/murry-salby/
SebH just parrots warmist talking points, and either rarely ever backs them up, or sometimes pretends to by giving references to other purveyors of said talking points.
PS, it is noted that yet again, you are totally INCAPABLE of countering one thing I have said .
Sad, EMPTY seb.
I have always found it curious that the gullible believers are willing to believe that the imminent melting of, say, the Greenland ice shelf would raise sea levels because modern CO2 levels are so much higher than before. This depending on the ice cores showing the last 800,000 years. Since temperatures in previous interglacials have been 2-3℃ above present for thousands of years at a time you must wonder about the ability to think rationally (if any).
Do you think sea levels were the same in those “thousands of years” as they are today? Do you think the ice melting in those times didn’t cause any sea level rise?
How about a link to data that support your contention, SebH? Or is that too much to ask?
You know, like Kenneth Richard does, and many others of us frequently do, though to a lesser extent.
Are you too lazy or ignorant? Or do you just know that since your arguments are worthless nonsense, and there is nothing to support them, there’s no point in even trying? I’m guessing it’s mostly the latter.
“Do you think the ice melting in those times didn’t cause any sea level rise”
You mean the “Neoglaciation”, when most of the worlds non-polar glaciers were formed?
Is that the “ice melting” that you are talking about, seb ??
You do know that temperature-wise, we are pretty much only a small blip above the COLDEST period in 10,000 years, don’t you seb?
You do know that Arctic sea ice is only just a small amount down from its most extreme extent in 10,000 years, don’t you seb?
https://s19.postimg.org/a2p8qx7oz/Arctic-_Sea-_Ice-_Changes-_Chukchi-_Sea-_Yamamoto-2017.jpg
https://s19.postimg.org/v6om69bj7/Arctic-_Sea-_Ice-_Extent-_North-of-_Iceland-3000-_Years-_Moffa-_S_nchez-.jpg
You do know that Greenland ice area is just a tiny snip down from the highest extent in 8000+ years, don’t you seb?
https://s19.postimg.org/ceo16fi7n/Greenland-Ice-Sheet-Briner.jpg
You do know that the Antarctic has been COOLING for basically all of the last 2000 years, don’t you seb?
https://s19.postimg.org/nn6qmzrb7/antarcticacooling.gif
Or are you going to continue with your gross DENIALISM of facts and data?
Okay, here is another view from a sceptic layman.
I once attempted a layman calculation on how much landbourne ice must melt to raise global sea level by 1 metre. I came to the conclusion that 400,000 cubic kilometres of ice would do the job nicely. The interesting part was how much energy is required to achieve this. The isothermal melting of ice requires some 334 kilojoules per kilogram at 273.16 K. That figure applies only to the change of state from solid to liquid between the temperatures of -0.01C to +0.01C (or from 273.14K to 273.16K). But most of the ice on Antarctica is way below this temperature (like -50C) and for every degree below freezing each kilogram of ice will require a further average of some 2 kilojoules per degree more. To cut a long story short I reached the grand total of 121,454,545,500,000,000,000 kilojoules of energy.
The next problem was how to deliver this energy to the ice. Can’t use the sea, the ice is on land! I picked a time scale of 20 years, (twice the then alarmist time of 10 years) and derived a figure of 20,000 WATTS PER SQUARE METRE! The sun would have to go Nova to do that. If the time scale was extended to 10,000 years then it is possible. Alarmists never come back with any math, just waffle on how the sea is going to burrow under the ice. Suggesting that this means water must run UPHILL gets no response.
Or, they just point out that if East Antarctica were to melt completely, it would raise sea levels by 50 meters. There. They just debunked you.
Time scale please. 20 million cubic kilometres of ice can’t melt over night, no ways!
But Richard III, in the virtual fantasy world of modeled climate cAGW alarmists know it can, and at ever accelerating rates. 😀
OK now sing the cAGW hymn …
😃
“The sky is falling!
The sky is falling!
Run! Run! Run,
The sky is falling…”
😃
Yeah, tom0mason, I know, but it’s the kid’s cartoon face at the head of this article that got to me.
They don’t understand enough to giggle at it like we can.
This may be interesting. Found it in search (dictionary) re evaporation.
the act or process of evaporating:
a : change from a liquid to a vapor
• evaporation of water
• But warming increases the evaporation of ocean water, which could increase the snowfall on the Arctic and Antarctic ice sheets, remove water from the ocean, and lower sea level.
• —Jack M. Hollander
To the sincere scientists commenting on this site,
Thank you. I am not a scientist, just a deplorable American soaking up the expertise your years of training and field work has produced.
I wish to make a contribution to your conversation.
One of you is a propagandist, whose goal is to sow confusion and misinformation on behalf of his (undisclosed) masters. His writing style would be recognized by any North Korean government official. In our modern era, the master was Goerbels.
Therefore, I propose that the screen name of “SebastianH” should be changed by the editor to “Tokyo Rose”. That way even when sea surface temperatures drop to the point the USS Missouri can no longer be comfortably visited by tourists in Tokyo Bay, “Seb/Tokyo Rose”, can comment “Why don’t you denier boys just surrender? You are disproven at every turn!”
In lieu of his behavior here vs. the behavior of propaganda-promoting bigots in the Third Reich, I don’t agree that we should be comparing SebastianH to Goebbels or to anyone who instituted ethnic genocide. I don’t think SebastianH has “masters”. Instead, he has fallen for and believes in the quite popular narrative that presumes humans can and do exert fundamental control over the Earth system. The belief in human control of ozone, seawater alkalinity, species extinctions, precipitation, glacier melt, sea level rise, and ocean temperatures emanate from a zeitgeist, and less from allegiance to a cause.
Oh no, another NOT-extinct animal.
http://www.news.com.au/lifestyle/real-life/extinct-possum-back-from-the-dead/news-story/b8d43499f26ac70e0c34394e66b1244d
29,999 to go (just for this year) 😉
Waiting for someone to name any of them 😉
On second thought, don’t touch that thermostat just yet.
Greenie activists invariably cause harm.
http://www.news.com.au/travel/world-travel/south-america/true-extent-of-greenpeace-damage-to-nazca-lines-revealed/news-story/383ccdd3e476edfebcfcbdc2af005f48
The reason Al Gore’s prediction that CO2 causes global warming is wrong is because CO2 can’t. The Beer-Lambert Law, the basis of spectrographic analysis puts an absolute upper limit on how much infrared CO2 can absorb.
Since the warmists assert CO2 is the cause then Co2 rises first, and after some lag time temperatures rise.
But the 100 ice core samples in Greenland and Antarctica going back 800,000 years including over two dozen inter-glacials when large differences in CO2 levels and temperatures were measured. These ice cores show the exact opposite chain of causation.
After temperatures rise for about 1000 years then CO2 levels start rising. After temperatures start falling by around 1000 years then CO2 levels start falling. Ergo, CO2 does not cause global warming, as it is an effect of temperature increases. This is exactly what the Beer-Lambert Law predicts, that CO2 stops absorbing infrared radiation at under 100 PPM in our atmosphere.
CO2 is instead the basis of all plant life on Earth you carbon based life form, and it is the greatest plant fertilizer in the world, especially for desert plants as it enables them to use water much more efficiently. An effect NASA is seeing in in the Sahara from space.
2000 PPM is ideal and is the level master gardeners pump into their greenhouses.
Conclusion 1: We have a corrupt scientific environment where self-interested taxers and corporate interests buy so called scientists with Phds to tell lies for grant money. These “scientists” have been caught at least five times fudging the temperature records. Deliberately lying about the data is a mortal sin for anyone who claims to be a scientist.
Conclusion 2: We need to put as much CO2 as we can into the atmosphere.