By Erich Schaffer
Magic is all about illusion, and so is “climate science”. Nothing about the GHE is as it seems and so far the “critical” side has failed to see through it. No longer!
Examining the key question of surface emissivity, usually downplayed as a non-issue, reveals highly significant insights relativizing the common narrative and revealing another profound flaw in the theory. Eventually this will lead to a totally disruptive Eureka moment.
Did you know that even the moon has a GHE? If we adapt our “GHE formula” to the circumstances on the moon, we can easily calculate the maximum temperature it should yield at the equator (with the sun at the zenith). All we need to do is to allow for the specific albedo (~0.12) and the amount of solar radiation, which is about 1368W/m2.
(1368 * ((1-0.12) / 1) / 5.67e-8) ^0.25 = 381.7°K
Since the albedo is a bit uncertain (in the 0.11 to 0.13 range), let us just say 382°K straight. So the moon, at the equator, should theoretically yield a temperature of up to 382°K. The observed (average) maximum temperature however is about 394K [1][2][3][4], 12°K hotter than it should be. The same formula that tells us Earth had a GHE of 33°K, suggests 12°K of GHE on the moon. Houston, there is a problem! By the way, if the albedo was 0.3, like that of Earth, the formula would give us 360.5°K in this case, with a GHE of 33.5°K. Sounds strangely familiar, right?
Of course we know there is NO GHE on the moon, since it does not hold an atmosphere. Instead there must be something wrong with our theoretical approach, the formula itself. And if the very formula that determines the GHE of Earth is wrong, as just demonstrated, it might be about time to ring the alarm bells.
What went wrong?
There are two ways to get to the correct result with regard to the moon. First we could simply ignore the albedo, or set it to zero respectively, and then the formula gives the correct result of 394°K. This is pretty odd, since we know the albedo is real and ignoring it is wrong, and yet it seems to work. That is why the second approach makes way more sense. Next to including an albedo of 0.12, giving us an absorptivity of 0.88, we also assume an emissivity of 0.88, so that the two cancel each other out. Then again the result is 394°°K and everything is fine. In fact, an emissivity of 0.88 is the only value consistent with an albedo of 0.12 and an observed temperature of 394°K.
The mistake we initially made is easy to identify. We started with assuming an emissivity of 1, while in reality it is far lower. Such a mistake will always give you a calculative temperature which is too low, and thus an erroneous “GHE”. Bearing that potentially fatal mistake in mind, how do leading climate experts around the globe account for it? They say emissivity is 1, or so close to 1 that it is negligible, and certainly there was no reason to question it any further.
This unawareness carries well into the “critical” arena, where the question would usually be resolved by looking up text books. It turns out, this is totally insufficient since a) text books are mostly wrong and b) it does not help understanding the nature of the problem. It is pretty odd, given that what I am going to reveal is really climate science 101.If you don’t know that, you know nothing! And it seems no one knows.
So what is the surface emissivity?
It should be easy to answer since NASA is operating some research projects on the subject, with satellites “measuring” surface emissivity. Measuring may be a bit too much, since the actual data need interpretation in the context of models and so on. Anyhow, those measurements show a quite significant deviation from 1, especially with arid regions.[5]:
Now we would only need to calculate a weighted average of these data and we would finally have a definite answer on what surface emissivity of Earth is, right? WRONG!
Regrettably it is far more complicated, and, spoiler alert, ironically much simpler eventually in the end (we’ll get to that shortly).
Inadequate global surface emissivity data
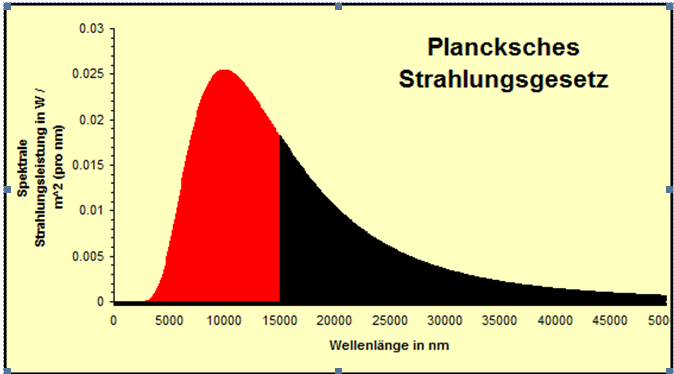
There are two huge issues with these data. First, quite obviously, water has been completely exempt and since it covers 71% of the planet, we can not ignore it. Second, the sensors usually top out at 15 µm (or less) and that leaves around 50% of the emissions spectrum at 288°K unchecked, as the chart below shows (black being the uncovered range).
The satellite data thus only cover 50% of 29%, or about 15% of global surface emissivity, giving zero information on the remaining 85%. This is totally insufficient, like predicting the US presidential election by only polling California. However, the problems we encounter ironically also lead the way to a solution.
A sunset over water is a beautiful sight. You see the sun over the horizon, and a strong reflection of the sun in the water. It would never look anything like it if the sun was higher up in the sky. Of course there is a reason for it, a law of physics, and that is exactly what we are after.
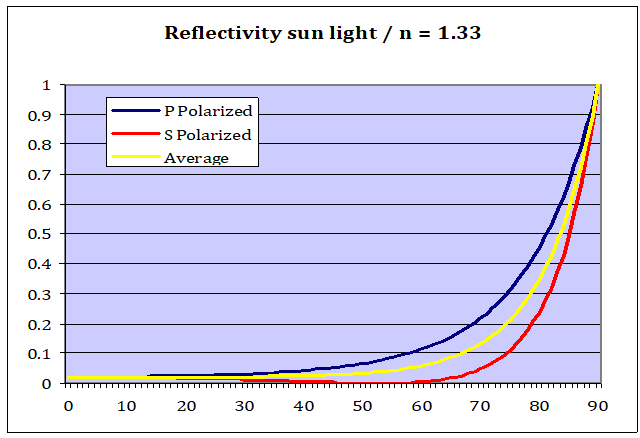
Fresnel equations allow us to determine precisely how much light is getting reflected on the surface of water, depending on the angle of incidence. I will not try to explore the formulas themselves, as they look quite complicated. Thank God they are not so hard to apply. All you need to know is the refractive index of water with regard to visible light (N = 1.33)[6][7], that of air (N=1) and then you get two results for s- and p- polarized light. Then you just take the average of those two curves and you get the final result.
A chart tells us more than a thousand words:
With the sun at the zenith, or anything near to it, water reflects only 2% of sunlight. But if the sun is close to the horizon, shining onto the water at a flat angle, most of sun light gets reflected, which is one of the reasons why sun sets look so beautiful.
Physically speaking sunlight is nothing but electromagnet radiation, just like LWIR, and thus the same physics apply. We only have to adapt the formula slightly to show how well water emits LWIR. First we need to know the appropriate refractive index in the LW range (N=1.27)[9] and then we just invert the result, since we do not search for radiation reflected, but rather what is being emitted.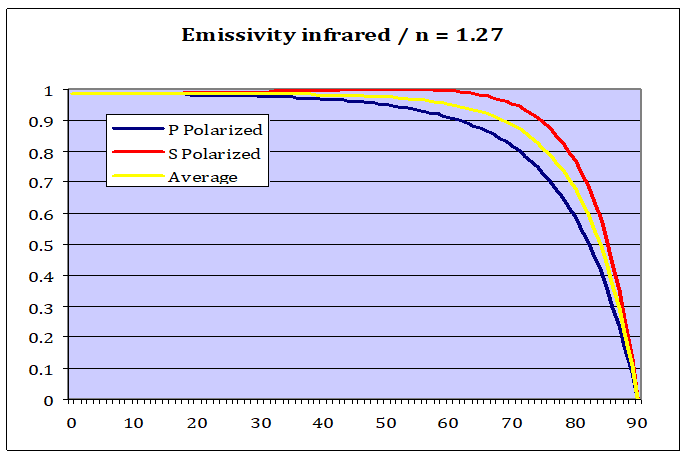
As we can see water is an excellent vertical emitter, with an emissivity of 0.986. This number so close to 1 that you could say the difference was indeed negligible. But that is only part of the truth. With flatter angles the picture changes dramatically and finally turns to 0 emissivity towards the horizon.
Satellites do not measure water emissivity
At this point it should become clear why satellites do not measure water emissivity. To minimize atmospheric disturbance, satellites need to look straight down onto the surface, which in this case is kind of pointless. The more interesting data could only be gathered by looking “sideways”, which satellites are very bad in. Even then, water is a very homogeneous surface type, which renders global observation obsolete, while on the other side we a have a solid theoretic approach. As far as empirical testing is concerned, 10 years ago “scienceofdoom” made a nice summary of research on the subject.[10]
If you google “emissivity of water” you will get all kinds of results. Given the complexity of the subject (including the political aspect) it is quite understandable. Regrettably this means you will have to figure it out yourself, which is mainly a mathematical challenge. The Fresnel equation tells us how water emits at a certain angle, but to get the hemispheric emissivity (we live in a 3 dimensional world) you will need to weight every gradient accordingly and also include Lambert’s cosine law. If I do all that, the result is 0.944.
Is this the final answer? I am not so certain! Anyone good in physics, or mathematics is invited to assist. One of the causes of doubt is, that German wikipedia [11], with reference to a noble German text book[12], has it at 0.91. Maybe I made a mistake after all. Then, just recently, I stumbled over an article stating “the emissivity of far-IR by the oceans is only about 89% of the 100% “efficiency” of emission/absorption of a true blackbody”[13], thereby suggesting a relatively larger refractive index in the far-IR (15-100µm). So I started again and with the help from a very useful site[14] calculated the average refractive index for the whole LWIR spectrum, which turned out to be N = 1.33, exactly the same as with SW radiation. With N = 1.33 my result for hemispheric emissivity drops to 0.934. By the way, I get 0.9 or 90% for the 15-100µm of far IR range, still relatively consistent with the 89% quoted above.
Kiehl/Trenberth fake science
All this may sound rather complicated and in the end there is still this sour taste of uncertainty. We know for sure however, that surface emissivity, especially with regard to water, is significantly lower than 1. With an emissivity of 0.94 a surface at 288°K emits 367W/m2, not 390. This alone shoves off 23W/m2 from the GHE at least and exposes the infamous “Kiehl, Trenberth diagram”, where they claim 390W/m2 of surface emission (396W/m2 in later editions), as fake science. That’s it!
Did I forget something?
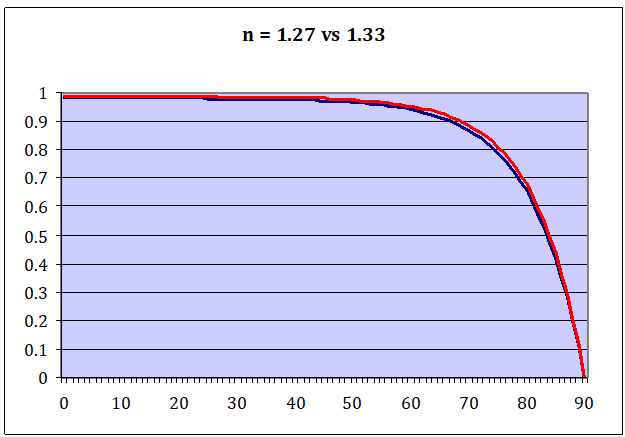
Oh yes, the big revelation. At this point we achieved more than we ever imagined, we just have not realized it yet. If we wind back to our Fresnel charts, there is an opportunity we missed. I did show reflectivity of water with regard to solar radiation and if we invert the chart, we get the result for absorptivity.
In the logical next step, we can directly compare absorptivity with emissivity and, as we can see, they are almost identical. That is if we assume N = 1.27 for LWIR, which is in line with experimental observations which exclude far-IR. As named before, including far-IR would move N likely up to 1.33, with absorptivity and emissivity then being perfectly identical.
What is the temperature of a body when absorptivity and emissivity are equal at given solar radiation?
(342 * (x / x) / 5.67e-8) ^0.25 = 278.7°K
GHE only 10°K
In other words, if there was no atmosphere, just the surface as it is (excluding any dynamic changes, ceteris paribus), the surface of Earth would take on the temperature of 278.7K. If we allow for N = 1.27, thus the little asymmetry between the curves, the temperature would drop straight by 0.7°K to 278°K . Without an atmosphere, Earth would be 10°K colder.
Or, alternatively spoken, the GHE is 10°K in size!
It is a revelation you may want to let sink, or protest respectively, but it is true. Just like with the initial example of the moon, the surface of Earth absorptivity and emissivity largely cancel each other out. This is not a law of physics, as Kirchhoff’s law only applies to identical wave lengths. But as much as there is variation in both absorptivity and emissivity with different wave lengths, the general tendency is for both of them to be more or less equal, especially with regard to wide spectra.[15]
Plenty of flaws – huge GHE hoax
The 33°K GHE narrative by comparison is build on a few “imprecisions”, so it seems. There is the surface emissivity = 1 mistake, there is the formal impossibility of counting cloud albedo to the “surface”, while at the same time denying the sheer existence of clouds in terms of emissivity. And then there are also plenty of flaws in the quantification of radiative effects, especially with regard to the CRE, that I have dealt with deeply in the previous article. All these “imprecisions” point in the same direction, certainly not accidentally so, and all together they accumulate to a huge GHE hoax.
It is a hoax as far as the apologetic side of “global warming” is concerned, but for the “critical” side it is an appalling failure. I have absolutely no understanding for how you can deal with the fiddliest questions of the science, polar bear populations, or Greta Thunberg’s pigtails, but totally miss out on the core blunder.
Difference between GHGE and GHE
To be accurate, the GHGE (greenhouse gas effect) needs to be distinguished from the GHE itself. The 278°K are true for the surface alone, and the 10°K GHE is what the atmosphere does as a whole. Of course it is perfectly thinkable there are components within the atmosphere which reduce the temperature of Earth, and then you can attribute more than just 10°K of GHE to GHGs.
If for instance clouds would cool the planet by 5°K, then we would arguably need 15°K of GHGE to get us back up to 288°K in the end. The global warming narrative thus interestingly takes relatively little harm, and can still prevail. The only precondition it needs is a significant net negative CRE. That of course is another story.
Footnotes
[1] https://lunarpedia.org/w/Lunar_Temperature
[2] https://www.nasa.gov/pdf/203096main_TEC%20Splinter-Thermal%20control.pdf
[3] https://www.sciencedirect.com/science/article/pii/S0019103516304869
[4] Actual maximum temperatures can reach over 400K, which is due to some craters serving as a kind of parabolic reflectors
[5] https://www.mdpi.com/2072-4292/10/7/1027/htm
[6] https://pixabay.com/de/photos/hamilton-island-australia-sun-set-585659/
[7] https://en.wikipedia.org/wiki/List_of_refractive_indices
[8] https://refractiveindex.info/?shelf=main&book=H2O&page=Hale
[9] N=1.27 is consistent with measurements on the subject. These measurements yet exclude the far long wave range. A total weighted spectral average according to the data here (https://refractiveindex.info/?shelf=main&book=H2O&page=Hale), would rather elevate N to 1.33, meaning identical Ns for LW and SW radiation.
[10] https://scienceofdoom.com/2010/12/27/emissivity-of-the-ocean/
[11] https://de.wikipedia.org/wiki/Emissionsgrad
[12] H. D. Baehr, K. Stephan: Wärme- und Stoffübertragung. 4. Auflage. Springer-Verlag, Berlin 2004, ISBN 3-540-40130-X (Kap. 5: Wärmestrahlung)
[13] http://hockeyschtick.blogspot.com/2014/11/new-paper-finds-huge-false-physical.html
[14] https://refractiveindex.info/?shelf=main&book=H2O&page=Hale
[15] Ironically NASA fully acknowledges this. NASA does not really measure the surface temperature of the moon, rather they measure radiation emitted with a satellite. To determine the actual temperature, they need to assume a certain emissivity. Essentially they simply reverse the formula I used above. The only way they can get to 394°K is by assuming absorptivity = emissivity. And they need to do this in order to get reasonable scientific results. When it comes to “climate science” however, they forget about science and stick rather to the emissivity = 1 myth.






A decade ago, Charles Anderson wrote about the “GHE” of the moon and it’s relevance to the effect seen on Earth, pointing out that even the moon appears to have one, despite no gasses and no convection. NASA had to calculate it when sending men to the moon. They know what causes it, and that it isn’t CO2.
https://objectivistindividualist.blogspot.com/2010/06/moon-effect-called-greenhouse-effect-on.html
“Heat convection in 3-dimensions creates an effect that looks like the greenhouse effect. Similar effects are observed for all of the planets.
It appears that if any “greenhouse effect” occurs due to CO2 in our atmosphere, that effect is very small compared to the 3-dimensional effects of distributed heat with convection heat transfer. That this is so has long been known by NASA, which nonetheless has played a very major role in the promotion of AGW alarmism on the basis of greenhouse gases!”
See also here.
http://web.archive.org/web/20200411025831/http://www.ilovemycarbondioxide.com/pdf/Greenhouse_Effect_on_the_Moon.pdf
Anderson has multiple posts on blackbodies and energy balance, and he is a physicist who’s company deals in energy transfer for a living.
Seemingly the same conclusion, but otherwise there is not much in common. I mean the fact that temperatures are lagging behind insolation is quite trivial and I do not see why one would want to call this “GHE”. In fact I read the article a while ago (seems like I have read the whole internet by now, LOL). No, it is all about getting emissivity right.
Btw., is it just my impression, or are people really just reading the first 3 paragraphs?!
Sorry, but the claim that the temperature of the moon is 394°C is NOT supported by your links. The middle one says:
“equatorial landing site would result in surface
temperature of up to 394 K plus full sun
This is NOT the average temperature of the planet. It is not even the average temperature of the equator.
It is the PEAK EQUATORIAL TEMPERATURE.
And since the claim of a 394K temperature is central to your hypothesis, I fear your entire argument collapses.
You might enjoy my post on the subject, “The Moon Is A Cold Mistress”.
http://wattsupwiththat.com/2012/01/08/the-moon-is-a-cold-mistress/
In it you can discover that the moon’s average temperature is nowhere near 394K …
My best to you,
w.
Thanks, Willis. I think Erich means that the max temperature reached on the moon, at the point exposed to direct sunlight, is 394°K. I’ve sent him an email to get his clarification on this point.
Thanks, Pierre.
But it is clear from both my links that the 394K was a predicted high temperature, with the actual turning out to be lower, while the actual low was higher than the predicted low.
To the side of the temperature illustration in the Hertzberg paper, we read. “The filled-in blue and orange zones depict the deviation between observed and predicted temperatures in the NASA experiments.”‘
The point of both, as I understand it, was to show that the estimation of temperature (average or not) using flawed assumptions gives the wrong answer. (It would be helpful if they provided original references. They may have, and the info in them was changed, but that’s another can of worms.)
Good thing for the astronauts NASA didn’t just rely on calculations, but also made measurements.
“For a surface with the sun directly overhead, for example a horizontal region near the equator at lunar noon, I is the solar constant in Earth’s neighborhood, about 1366 W/m^2, minus the portion reflected. Since the emissivity is close to 1 minus the reflectance, those two terms cancel out, and inverting the equation gives the maximum day-time high on the Moon: 394 K or about 120 degrees C.” https://lunarpedia.org/w/Lunar_Temperature
Oh, good. Independent confirmation. Thanks. (also I now have one in moderation.)
“Daytime maximum temperatures are sensitive to the albedo of the surface and are ∼387–397 K at the equator,…” https://www.sciencedirect.com/science/article/pii/S0019103516304869
Dear Willis
I have read your article a while ago, and to be honest, I did not fully agree back then and that has not changed.
“Given that the moon must be radiating about 304 W/m2 of energy to space to balance the incoming energy, the corresponding blackbody lunar temperature given by the S-B equation is about half a degree Celsius.”
No it is not, since..
(304 / 5.67e-8)^0.25 = 270.5K or -2.5°C
The basic problem you are dealing with is the power 1 vs. power 4 issue. If you had a disc with 2 sides, one at 200K and the other at 400K, they would emit like ((200^4 + 400^4)/2) ^0.25 = 341,5K average. That is while the arithmetic average is only 300K. It is a simple problem which can easily be understood, and of course it applies to the moon (to a small extend also to Earth, which is probably the reason why Kiehl/Trenberth later adjusted their surface emissions from 390 to 396W/m2, always trying to squeeze out a little more GHE).
Thus, reasonably, one should average the surface temperatures based on the 4th power. I did invest quite some time trying it and my result was ~276K. It was a very consistent result, given the uneven surface of the moon exceeds that of a smooth sphere by a few percent. With consistent I mean it would almost perfectly match the temperature of a PBB (perfect black body) of 278.7K. Anyhow, that would be a lengthy discussion and I skipped it for good reasons.
It is so much easier to just take the maximum temperatures, as the subject of emissivity applies either way. And as pointed out it is about average maximum temperatures (as opposed to local maximum temperatures that can go beyond 400K). 394K is indeed the correct temperature (+/- something), as named in the references. Beyond that I still have detailed Diviner (temperature) maps on my hard drive, which clearly show maximum temperatures > 390K on average at the equator (the link below gives one example, but I can not find to full set anymore online). Such temperatures can only be attained when emissivity is substantially lower than 1, which is a trivial fact of physics anyhow. Ignoring this deviation, let us call it LW-albedo to finally give it name, is pointless.
https://www.nasa.gov/mission_pages/LRO/multimedia/lro-gal-diviner.html
Furthermore, and I fully understand people do not read through the references, the 394K are neither “central”, nor is what I am saying a “hypothesis”. Fresnel equations are a well established facts of physics, one only needs to look it up. The same goes for the refractive indices of water. Which of course brings up the question why I seem the first to do it, on the “critical side” at least.
[…] Ref.: https://notrickszone.com/2020/09/27/plenty-of-physics-flaws-accumulate-into-a-huge-ghe-hoax-the-dark… […]
Sep 26, 2020 “CLIMATE LOCKDOWN” – The End Game Becomes Clear: Post-Human Future
Their hand is forced as the Global Warming narrative breaks down and the Modern Grand Solar Minimum goes mainstream.
https://youtu.be/Y81EOYIIN34
Thanks, Pierre. He’s built his whole case around the idea that:
“Since the albedo is a bit uncertain (in the 0.11 to 0.13 range), let us just say 382°K straight. So the moon, at the equator, should theoretically yield a temperature of up to 382°K. The observed (average) maximum temperature however is about 394°K [1][2][3][4], 12°K hotter than it should be.”
As you point out, however, equatorial temperatures do range all the way up to 397K (please tell Erich that using “°K” is a bad sign …).
Next, as he points out, local conditions can drive the temperature of the surface well above the S-B conditions. Ericc says (footnote 4):
“Actual maximum temperatures can reach over 400K, which is due to some craters serving as a kind of parabolic reflectors.”
This is true, and there is another reason for high temperatures. This is the variation in albedo in local lunar areas, depending on steepness, material, and physical form (regolith etc.)In some areas the local albedo can be as low as 0.6.
Max temperature is also affected by the type of material, with regolith (moon rock turned into powder by repeated meteorite strikes) getting ~ 25K hotter than exposed rock.
Finally, emissivity affects the S-B calculated maximum. In some areas it’s as low as 0.8. I’ll use 0.9.
SO: Using his formula and putting in the values for low emissivity (0.9) and low albedo (0.08), I get
(1368 * ((1-0.08) / .9) / 5.67e-8) ^0.25 ≈ 396K
This is in good agreement with your figures quoted from the Diviner experiment article of “∼387–397 K at the equator”.
So no, there’s no imaginary “greenhouse effect” going on with the moon.
My best to you, Pierre, and to Erich as well. Although his analysis is wrong, he is running the numbers himself. And that is the very best way to understand anything.
w.
PS—Excellent analysis of the Diviner Experiment below …
https://www2.physics.ox.ac.uk/sites/default/files/2012-03-08/2_thomas_pdf_10647.pdf
Here’s a reply from Erich, https://notrickszone.com/2020/09/27/plenty-of-physics-flaws-accumulate-into-a-huge-ghe-hoax-the-dark-secret-behind-surface-emissivity/#comment-1309016
Willis, you are being a bit unfair here.
I did NOT build the case around the moon, nor is my analysis wrong, nor did you even point out what should be wrong. I mean appart from wrongly assuming I would claim the average surface temperature of the moon was 394K.
I named the example of the moon for one good reason, since it demonstrates very well what fatal mistake it is to plainly assume emissivity = 1, or ignore the subject all over. I mean like you did in your wuwt article. You did not mention emissivity once! Or like it is being done when calculating the GHE or Earth.
Starting from there it seems we finally made some progress..
“SO: Using his formula and putting in the values for low emissivity (0.9) and low albedo (0.08), I get..”
Right, we need to allow for real emissivity to make any sense, which is what the lesson was all about. Eureka!
“(please tell Erich that using “°K” is a bad sign …)”
Yeah, Pierre will have to teach me that ;). There was no “°K” in the article i submitted. LOL
Re the moon not having an atmosphere … I guess technically it does although it is more correctly termed an exosphere. Somehow I ended up reading about it back in August and so when I read this post I thought I would give u folks a heads up.
I don’t vouch for the accuracy …. just a subject I had read about recently and thought I should share. Enjoy.
https://www.space.com/18067-moon-atmosphere.html#:~:text=On%20the%20moon%2C%20there%27s%20no%20air%20to%20breathe%2C,called%20an%20atmosphere.%20Technically%2C%20it%27s%20considered%20an%20exosphere.
Well, yes there are few gaseous atoms around the moon. But a) these are perfectly transparent by nature (Hydrogen, Helium, Argon, Neon) and b) so rare that will not even slow down any space probe orbiting moon in the long run. In terms of surface temperature they are a 100% irrelevant.
Well, yes there are few gaseous atoms around the moon. But a) these are perfectly transparent by nature (Hydrogen, Helium, Argon, Neon) and b) so rare that will not even slow down any space probe orbiting moon in the long run. In terms of surface temperature they are a 100% irrelevant.
All way too technical. Much easier to stick to the faith, as taught by Pippi Långstrump, that man-made CO2 will doom us all.
“What is the temperature of a body when absorptivity and emissivity are equal at given solar radiation?
(342 * (x / x) / 5.67e-8) ^0.25 = 278.7°K ”
Willis’s point remains valid. Given that the moon receives the same amount of solar radiation , the above number in your estimation should also apply to the moon. But it doesn’t. If you look at Vasavada et al. 2012 and also the Diviner radiometric measurements Paige et al. 2010 conducted by NASA See Vondrak et al. 2010, you will get the chart- Figure 5 on pg 10 of Nikolov and Zeller’s 1st paper where they spelled their names backward. In that Figure 5 you will see that the moon has a steady nightime temperature of ~ 110 K for 12 hours and a 12 hour daytime average temperature of ~ 278 K. This equates to an average temperature of 194K. Nickolov and Zeller did some complicated calculations which included heat storage of the moon’s regolith and they used the formula Temp of moon = .4 *([So*(1-albedo)/(SB constant * emissivity)] ^1/4) * [((1-n)^1/4) + (0.932 * n^1/4)] where So is the solar irradiance at TOA and n= the fraction of absorbed solar flux stotred into the the regolith through heat conduction. They found the ave. temperature of the moon to be 197.1 K. So my back of the envelope calculation of 194 K is only 3K difference. So this shows that the greenhouse effect of the earth atmosphere is at least 90 K. NASA apparently agrees with this because they developed a thermo physical model named TWO which was verified against borehole measurements on the moon surface.The TWO model calculated the moon’s average temperature to be 197.3 which differs from Nickolov and Zeller’s by only 0.2 K. The equation used by Nickolov and Zeller above is essentially the Stefan Boltzmann equation. However I still have much suspicion about using this equation to determine average temperatures. See Ross Mcleod https://principia-scientific.com/publications/Ross-GHE-Experiment.pdf
“So this shows that the greenhouse effect of the earth atmosphere is at least 90 K”
No, it is just ~10K!
In response to Alan Tomalty, sry
I have spent some years doing theoretical physics in this area (thermodynamics). I think you definitely have a point. I think your theory is sound from a physical point of view.
The emissivity is dependent on angle of the outgoing radiation. My interpretation of your theory is that the emitted power from a surface should be weighed with angle dependent emissivity.
Today when people apply SB they indirectly assume an angle independent emissivity (Lamberts cosine law is included in SB). If you go back to Planck´s famous “derivation” it is for a hole in a black box. The hole has no refractive index.
My guess is that when people measure temperature with a pyrometer, they try to keep the pyrometer perpendicular to the surface of the body.
I think your theory is very interesting, and it may very well explain a big part of earth´s “overtemperature”.
Another interesting aspect is that your theory should be possible to validate (or falsify) with experiments.
But, but … helical modelling of Greta Thunberg’s pigtails is important!
It could help unlock some aspects of string theory.
Thanks Erich for an illuminating article.
I’ve always found it intuitively unbelievable that removal of a 0.04% trace gas would change the atmosphere’s temperature by several degrees.
Tangentially, this paper by a fellow Austrian shows by careful experimtation that absorption of heat by pure CO2 is not different from that of air or argon:
https://www.allphyscon.ch/wordpress/wp-content/uploads/Allmendinger_Behaviour-of-Gases_IJPS-rev.pdf
Einstein asserted something similar from a theoretical POV:
https://ptolemy2.wordpress.com/2020/02/16/albert-einstein-said-no-to-co2-radiative-warming-of-the-atmosphere/
Sorry – Allmendinger is from Zurich
One more comment. I think it is rather straightforward to derive a modified SB equation based on an angle dependent emissivity.
Have you done that ? Want some input ?
You are invited to go through the formulas. Really, it is just the application of text book physics, which I hope to apply correctly.
a) the Fresnel equation. It has been a while that I converted this into Excel, but obviously the formula works.
s-polarized:
=($B$1*COS(C5)-$B$2*(1-($B$1/$B$2*SIN(C5))^2)^0.5) / ($B$1*COS(C5)+$B$2*(1-($B$1/$B$2*SIN(C5))^2)^0.5)
p-polarized:
=($B$1*(1-($B$1/$B$2*SIN(C5))^2)^0.5-$B$2*COS(C5)) / ($B$1*(1-($B$1/$B$2*SIN(C5))^2)^0.5+$B$2*COS(C5))
$B$1 = N1 = 1 = refractive index of air
$B$2 = N2 = 1.27 (or 1.33) = refractive index of water
C5 (and C6, C7..) is the respective angle
b) Planck’s law
I did not really deal with the formulas themselves, I only downloaded an Excel sheet for educational purposes that contaisn the formula. You only have to set the temperature the get the respective radiation spectrum.
c) finally you can combine this with the data provided by the site below. Note: you can enter specific wave lengths to get the resptive refractive index. If you go through it step by step for the whole range of LWIR for instance, you can calculate a weighted average refractive index, and with that you can calculate emissivity. Applying it on the SB-equation is the easiest task 😉
https://refractiveindex.info/?shelf=main&book=H2O&page=Hale
you can contact me over my spam mail (or ask Pierre for the proper email)
leitwolf_22 at yahoo.com
Then I could send you the Excel sheets right away.
Hi Erich,
These two resources will help you fix a few errors:
http://phzoe.com/2020/02/12/average-moon-temperature/
http://phzoe.com/2019/11/05/what-is-earths-surface-emissivity/
Best regards, -Zoe
Thx
a) Obviously I have little objections to an average emissivity of 0.93643 ;). Rather I think it is amazing how text book physics (or formulas respectively) give such a good approximation, given NASA is right.
b) Again, it is the problem of averaging by the power of 1 (thus arithemitically) what is actually a function by the power of 4.
Since you already averaged every single gradient I played a little trick on it. Assuming an average dark side temperature of 80K I determined the sun side average a = x*2 – 80, with x being the respective gradient average in your table. Then I took temperatures by the power of 4, multiplied them with the weightening factor you provided, added it all up, drew the 4th root and the result was 318.1K for the sun side.
((80^4 + 318.1^4)/2) ^0.25 = 276K (!!!)
Funny, isn’t it?
Is it valid to average radiation?
If you stood between 10C and 20C objects (of same material), you would feel 15C. But convert those temps to radiation, average them and then convert back to temperature, and you’ll have the wrong answer.
If you placed thermometers on every square meter of the moon, the average would be ~200K.
I just don’t think it’s valid to average radiative fluxes and then convert to temperature.
Hi Erich,
seems as if you have done the math. I agree with your model.
My thinking was to use the “standard” derivation of SB-law. They take the spectral radiance, multiply with Lamberts cosine(emission angle) and integrate over a half sphere.
In the derivation the emitting material has a refractive index of 1 (all angles). Suppose one assign a refractive index to the emitting material (the heat radiation trying to “get out” from the material sees a change a in refractiv index).
I think (not 100% sure) that one can take the radiance, multiply with the cosine and then multiply with the transmission factor according to Fresnels equations. Then integrate over a half sphere.
It would defenitly reduce the emitted power, since radiation that is not perpendicular to the interface will have a transmission coefficient below 1.
The emitted power will be less than an “uncritical” application of SB-law.
In my mind this is a very interesting idea. A bit surprised that this has not been highlighted before. I think your arguments are solid, and they are the same as the “standard” thinking in optics.
Question is how much do people overestimate the emission from e.g. a water surface when they apply SB (with the “perpendicular emission” applied as a constant for all angles). My guess is that it is a significant overestimation. This effect should be included – it is not marginal.
I think the ideas in this article was so interesting that I derived the emission from a cavity filled with a non-conducting material with refractive index >1.
Same derivation as the standard derivation of SB-law (which use n=1 in the derivation). Ends up with a bit complicated integrals that has to be integrated numerically.
What is clear from the formulas is that the emissivity tends to zero when the refractive index becomes large. It is also clear that the radiation lobe narrows, since only angles 1 , SB overestimates the emitted power.