The strong correlation between Galactic Cosmic Rays (GCRs) and cloud formation has for decades been postulated as a primary mechanism for solar-driven natural climate change. Concisely, “When the Sun is active fewer cosmic rays reach the Earth and, with fewer low clouds, the world warms up” (Svensmark et al., 2017). Since about 2000, however, this GCR-cloud correlation has been violated (solar activity has declined without accompanying GCR flux), leading many to question the link. A new paper suggests this post-2000 “violation” is actually “not…unexpected”, has occurred previously, and does not undermine the Sun-GCR/cloud explanation for naturally-driven climate change.
Veretenenko et al., 2018
Galactic Cosmic Rays and Low Clouds:
Possible Reasons for Correlation Reversal
“Indeed, cloudiness changes can strongly modulate fluxes of both incoming short-wave solar radiation and outgoing long-wave radiation of the Earth and the atmosphere and, thus, influence significantly the radiative-thermal balance of the atmosphere. High-level clouds contribute to the warming of the atmosphere, whereas low-level clouds contribute, as a rule, to its cooling. A net influx of radiation coming to the Earth’s surface under cloudy conditions depends on latitude, season and underlying surface. According to the data obtained from spaceborne experiments [Nimbus 7 Earth Radiation Budget experiment (N7ERB) and Earth Radiation Budget Experiment (ERBE)], when averaged over the globe, cloudiness reduces the input of solar radiation by 44.5–54.3 W·m−2 (depending on the season) and the emission of long-wave radiation to space by 23.6–34.7 W·m−2 [1, 2]. As a result, cloudiness decreases the global radiative heating of the atmosphere by 17.3–26.8 W·m−2.”
“Influence of galactic cosmic rays (GCRs) on cloud formation is suggested to be an important part of the mechanism of solar activity influence on weather and climate. A high positive correlation between low cloud amount and GCR fluxes was observed in the 1980s–1990s; however, in the early 2000s, it was violated. In this work, we consider a nature of long-term correlation links between cloud cover at middle latitudes and GCRs, as well as possible reasons for this correlation reversal. It was shown that the GCR-cloud links observed on the decadal time scale are indirect and caused by GCR effects on cyclonic activity which depend on epochs of the large-scale atmospheric circulation. The reversal of GCR-cloud correlation in the 2000s seems to be due to a sharp weakening of the Arctic and Antarctic stratospheric polar vortices, which results in the change of the troposphere-stratosphere coupling and, then, of GCR contribution to the development of extratropical cyclogenesis.”
“Correlation links observed between lower atmosphere characteristics and phenomena related to solar activity may weaken, disappear and even change sign depending on time period. So, a violation of the cloud-GCR link in the 2000s is not an extraordinary event. Herman and Goldberg [56] suggested that a reason for temporal variability of solar-atmospheric links may be long-term processes of the Sun which do not influence sunspot numbers and/or some changes of atmospheric conditions. Veretenenko and Ogurtsov [42, 43] showed that temporal behavior of correlation links between surface pressure at extratropical latitudes and sunspot numbers is characterized by a roughly 60-year periodicity caused by changes in the epochs of the large-scale atmospheric circulation. The reversals of the correlation signs were found in the end of the nineteenth century, in the early 1920s, the 1950s and the early 1980s coinciding with climatic regime shifts at middle latitudes [57], as well as with the transitions between cold and warm epochs in the Arctic [58]. So, a violation of the cloud-GCR link in the 2000s seems not to be unexpected and may be associated with the next change of the circulation epochs resulting in the change of GCR contribution to extratropical cyclonic activity and, then, to cloud field formation.”
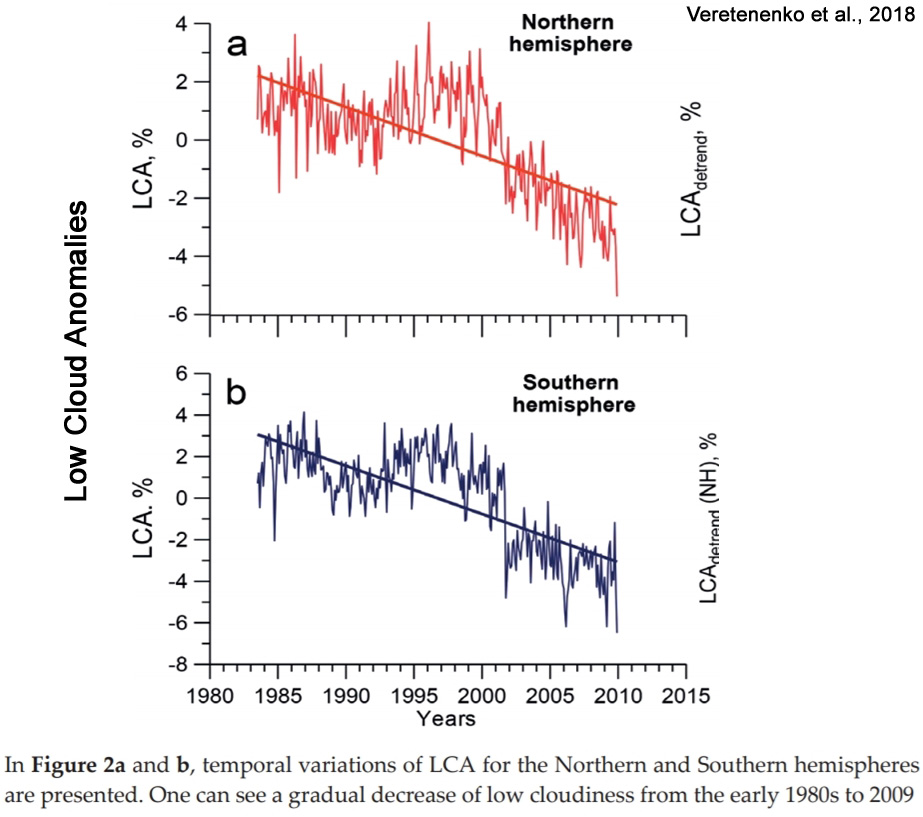
Image Source: Veretenenko et al., 2018
Cloud Radiative Forcing Can Explain 1980s-2000s Warming
Cloud cover changes dominate in altering the amount of solar radiation absorbed by the Earth’s surface (Stanhill et al., 2014; Mateos et al., 2014).
With fewer clouds, more solar radiation can be absorbed by the oceans rather than reflected back to space; this, in turn, leads to warming.
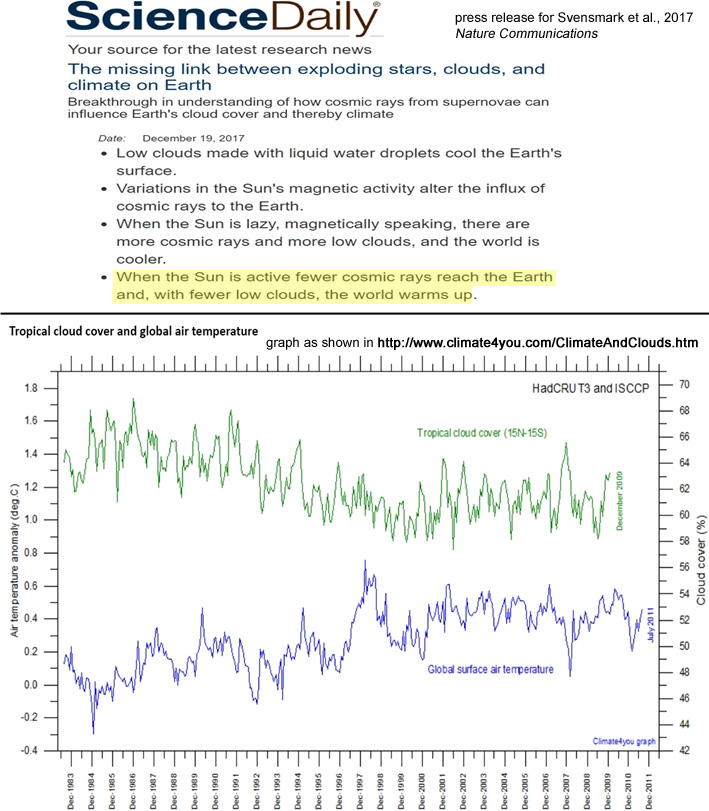
Image Source: Sciencedaily.com and Climate4you.com
Cloud cover changes and the concomitant alteration of surface solar heat absorption can therefore explain the 1980s to 2000s warming via the increase in absorbed solar radiation (Pinker et al., 2005; Pallé et al., 2004; Herman et al., 2013; Wang et al., 2012; Calbó et al., 2016; Kauppinen et al, 2014; McLean, 2014).
The GCR-Cloud “Missing Link” To Climate Change “Breakthrough”
There has recently been a scientific “breakthrough” in understanding the “missing link” between the Sun’s modulation of cosmic rays and thus cloud cover, supported by real-world observational evidence (3,100 hours of data sampling and controlled experimentation).
The following is an abbreviated list of 14 scientific papers supporting the Sunspot Activity→Cosmic Ray Flux→Cloud Cover Changes→Climate Changes conceptualization published within the last year.
Sciencedaily press release for Svensmark et al., 2017
The missing link between exploding stars, clouds, and climate on Earth
“Breakthrough in understanding of how cosmic rays from supernovae can influence Earth’s cloud cover and thereby climate”
“The new results reveal, both theoretically and experimentally, how interactions between ions and aerosols can accelerate the growth by adding material to the small aerosols and thereby help them survive to become cloud condensation nuclei. It gives a physical foundation to the large body of empirical evidence showing that Solar activity plays a role in variations in Earth’s climate. For example, the Medieval Warm Period around year 1000 AD and the cold period in the Little Ice Age 1300-1900 AD both fits with changes in Solar activity.”
“‘Finally we have the last piece of the puzzle explaining how particles from space affect climate on Earth. It gives an understanding of how changes caused by Solar activity or by super nova activity can change climate.’ says Henrik Svensmark, from DTU Space at the Technical University of Denmark, lead author of the study.
“Data was taken over a period of 2 years with total 3100 hours of data sampling. The results of the experiments agreed with the theoretical predictions.”
• Low clouds made with liquid water droplets cool the Earth’s surface.
•Variations in the Sun’s magnetic activity alter the influx of cosmic rays to the Earth.
•When the Sun is lazy, magnetically speaking, there are more cosmic rays and more low clouds, and the world is cooler.
•When the Sun is active fewer cosmic rays reach the Earth and, with fewer low clouds, the world warms up.
The implications of the study suggests that the mechanism can have affected:
• The climate changes observed during the 20th century
• The coolings and warmings of around 2°C that have occurred repeatedly over the past 10,000 years, as the Sun’s activity and the cosmic ray influx have varied.
• The much larger variations of up to 10°C occuring as the Sun and Earth travel through the Galaxy visiting regions with varying numbers of exploding stars.
“The spectral analysis of the sedimentological parameters reveals the significant periodicities (>95% significance) centering at ∼1067, ∼907, and ∼824 years. The long-term trends in the data suggest the possible fluctuation of Antarctic ice-sheet superimposed on global climatic fluctuations due to solar activity. … The curiosity of climate scientists arises on the mechanism of reaction of the climate system in response to the changes in solar forcing. There are two possible mechanisms proposed which work through the atmospheric processes. The first mechanism includes the action of the ozone layer by increasing more UV radiations with increased solar activity. It must have raised the temperature in the stratosphere which produces stronger winds in lower stratosphere and troposphere. These strong winds in the troposphere result in the relocation of pressure cells and storm tracks which ultimately disturbs the climate system (Schindell et al., 1999; Crosta et al., 2007). The second proposed mechanism considers the cosmic rays and cloud cover responsible for amplifying the climate forcing (Svensmark, 2000).”
“High solar activity is believed to be responsible for less cooling of the lower atmosphere due to reduced cloud cover (Marsh and Svensmar, 2000). Conversely, low solar activity is believed to provide additional cooling of the lower atmosphere. These two feedback mechanisms responsible for the climatic forcing due to solar activity may work alone or in conjugation and are also superposed to other climate forcing as well as variability of internal cycling (Rind, 2002). Further, the periodic increase in solar activity results in increased temperature in the lower atmosphere which causes melting of ice-sheets in the Antarctic region. It may further provide the periodicity in freshwater discharge in the Schirmacher lakes and hence regulates the depositional environment of the studies lake.”
“The results of this review point to the extreme value of CO2 to all life forms, but no role of CO2 in any significant change of the Earth’s climate. … There is no correlation of CO2 with temperature in any historical data set that was reviewed. The climate-change cooling over the 1940–1975 time period of the Modern Warming period was shown to be influenced by a combination of solar factors. The cause of the Medieval Warm Period and the Little Ice Age climate changes was the solar magnetic field and cosmic ray connection. When the solar magnetic field is strong, it acts as a barrier to cosmic rays entering the Earth’s atmosphere, clouds decrease and the Earth warms. Conversely when the solar magnetic field is weak, there is no barrier to cosmic rays—they greatly increase large areas of low-level clouds, increasing the Earth’s albedo and the planet cools.”
“Nevertheless, these results over this long period strongly suggest that the solar magnetic feld/cosmic ray interaction is the primary cause of major climate-change events over the past 9400 years of the interglacial period. The 35-year cool period within the current Modern Warming was an example where the Gleissberg cycle imposed only a modest impact on the existing strength of the magnetic feld that was in place. The current Modern Warming will continue until the strength of the Sun’s magnetic field declines.”
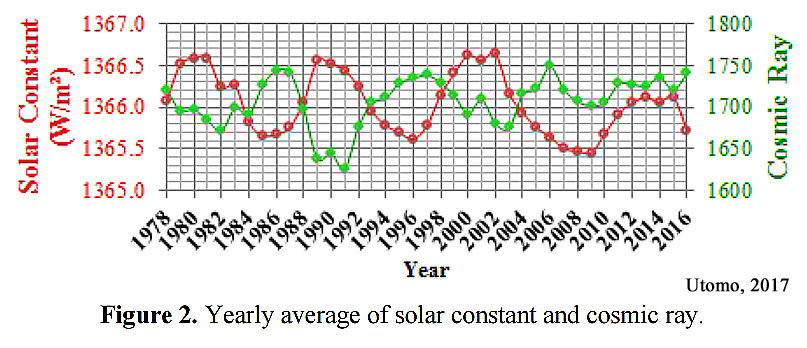
“A similar result was also found for the relationship between solar activity and cosmic ray flux with a negative correlation, i.e. 0.69/year. When solar activities decrease, the clouds cover rate increase due-0.61/month and – to secondary ions produced by cosmic rays. The increase in the cloud cover rate causes the decrease in solar constant value and solar radiation on the earth’s surface. … The increase in the formation rate of cloud would affect the decrease in the intensity of solar radiation reaching the Earth’s surface. The relationship between cosmic rays and solar constant is an “opposite” relationship because of the negative correlation type (r < 0). The phenomenon of “opposite” is in a good agreement with the result by Svensmark (1997) who found a correlation between temperature and global cloud coverage with the cosmic rays… [T]he climate also depends on variations in the flux of solar energy received by the earth’s surface. Variation in the solar energy flux is caused by variations in solar activity cycle. Thus the climate is a manifestation of how solar radiation is absorbed, redistributed by the atmosphere, land and oceans, and ultimately radiated back into space. Every variation of solar energy received at the earth’s surface and reradiated by the earth into space will have a direct impact on climate change on Earth.”
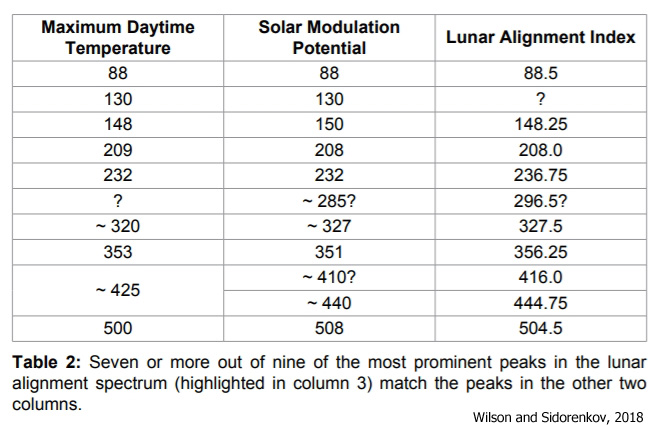“Hence, the solar connection between Tm and ϕm can be summarized using a heuristic luni-solar model like that shown in Figure 6. Firstly, the model proposes that there must be some, as yet, unknown factor associated with the level of solar activity on the Sun (e.g. possibly the overall level GCR hitting the Earth) that is producing long-term systematic changes in the amount and/or type of regional cloud cover. Secondly, the model proposes that the resulting changes in regional cloud cover lead to variations in the temperature differences between the tropics and the poles which, in turn, result in changes to the peak strength of the zonal tropical winds. Thirdly, the model further proposes that it is the long-term changes in the amount and/or type of regional cloud cover, combined with the variations in the temperature differences between the tropics and the poles that lead to the long-term changes in the poleward energy and momentum flux. And finally, the model proposes that it is this flux which governs the rate at which the Earth warms and cools, and hence, determines the long-term changes in the world mean temperature.”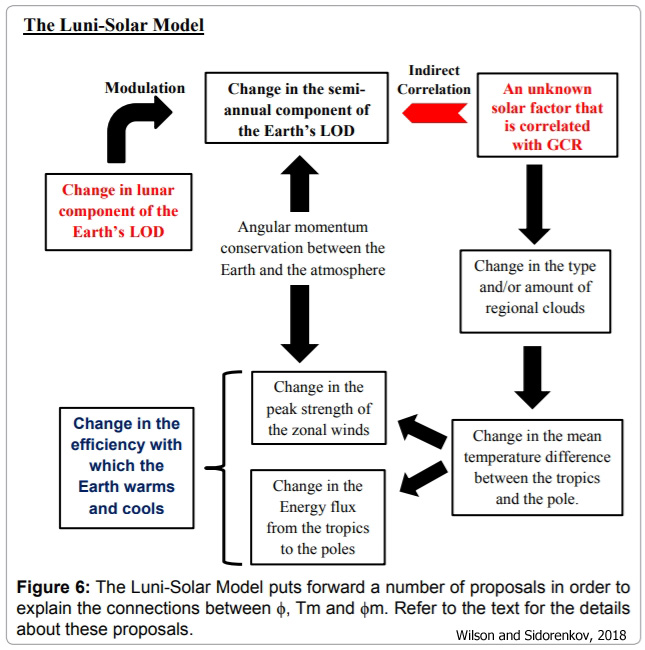
Padovani et al. at https://arxiv.org/pdf/1809.04168.pdf
note an extremely interesting GCR process in star formation clouds.
Again it looks like weather and star formation activity is a galactic phenomenon, or rather qualitatively different grades thereof.
Great link!
A great link, indeed. The GCR influence on terrestrial climate over millions of years was articulated by Svensmark and Calder in their marvelous book “The Chilling Stars.” This hypothesis, for which there is increasing empirical evidence, constitutes a major event in environmental thinking, insofar as it reveals how long-term processes of the Milky Way galaxy and beyond affect climate and thereby terrestrial evolution. The Solar System is our immediate neighborhood, but Earth’s development continues to be affected by events in the far vaster domain.
And the cloud error in climate models is 140 times greater than the CO2 non-warming signal AGW scammers are attempting to fabricate.
https://wattsupwiththat.com/2016/11/22/the-needle-in-the-haystack-pat-franks-devastating-expose-of-climate-model-error/
Thanks, spike. That’s a keeper.
This is becoming overwhelming. I look forward to it being reported on the BBC…
Don’t hold your breath, dennis!
Incidentally, Pierre is citing no fewer than 13 papers here. I wonder how long before seb turns up to tell us they’re all b******s and puts us all right! I can barely wait.
It’s funny that searching for a GCR cloud connection only brings up pseudoskeptic blogs as if that were an exclusive topic to their part of the internet.
13 papers, seb. How come you know better than them since your knowledge even of basic physics — as demonstrated on these pages day in day out — is non-existent?
A little humility, seb. Just for a minute believe that there are scientists who know more than you do and happen not to agree with you. I know it hurts when people think differently from you but learn to live with it. One day you will be glad you did because that way comes peace and understanding.
All that your way leads to is frustration, heart attacks, and mockery. And since you patently talk nonsense every time you post, the mockery will be well-deserved!
Here’s some good news
http://www.faz.net/agenturmeldungen/dpa/eu-kommission-laesst-vorschlag-fuer-klimaziel-2030-fallen-15810919.html
Looks like Señor Cañete saw some light!
The bad news is, there are any “climate targets” still in place!